《2025年南通小题课时作业本七年级数学上册苏科版》

25. (10分)已知含字母a,b的代数式是$3[a^{2}+2(b^{2}+ab - 2)]-3(a^{2}+2b^{2})-4(ab - a - 1)$.
(1)化简代数式；
(2)小红取a,b互为倒数的一对数值代入化简的代数式中,恰好计算得代数式的值等于0,那么小红所取的字母b的值等于多少？
(3)聪明的小刚从化简的代数式中发现,只要字母b取一个固定的数,无论字母a取何数,代数式的值恒为一个不变的数,那么小刚所取的字母b的值是多少呢？

答案： 25.
(1)原式$=3a^{2}+6b^{2}+6ab-12-3a^{2}-6b^{2}-4ab+4a+4=2ab+4a-8$.
(2)因为a,b互为倒数,所以$ab=1$,
所以$2+4a-8=0$,解得$a=\frac{3}{2}$,所以$b=\frac{2}{3}$.
(3)由
(1)知,原式$=2ab+4a-8=(2b+4)a-8$.
因为结果与a的值无关,所以$2b+4=0$,
解得$b=-2$.

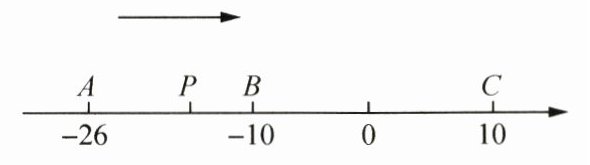
26. (10分)已知数轴上有A,B,C三点,分别表示有理数-26,-10,10,动点P从点A出发,以每秒1个单位长度的速度向终点C移动,设点P的移动时间为t s.
(1)用含t的代数式表示点P到点A和点C的距离：PA = ______,PC = ______；
(2)当点P运动到点B时,点Q从点A出发,以每秒3个单位长度的速度向点C运动,点Q到达点C后,再立即以同样的速度返回点A.当点Q开始运动后,请用含t的代数式表示P,Q两点间的距离.

答案： 26.
(1)t $36-t$
(2)当$16≤t≤24$时,$PQ=t-3(t-16)=48-2t$;
当$24＜t≤28$时,$PQ=3(t-16)-t=2t-48$;
当$28＜t≤30$时,$PQ=72-3(t-16)-t=120-4t$;
当$30＜t≤36$时,$PQ=t-[72-3(t-16)]=4t-120$.
综上,$PQ=\begin{cases}48-2t,\quad16≤t≤24, \\2t-48,\quad24＜t≤28, \\120-4t,\quad28＜t≤30, \\4t-120,\quad30＜t≤36. \end{cases}$