第107页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
7 (2025 南通启东期末)如图,已知∠AOB,以 OA 为边作∠AOC,使∠BOC= $\frac{1}{2}$∠AOB,则下列结论中成立的是(
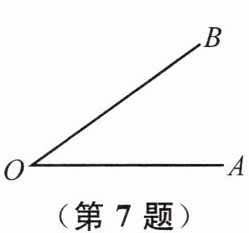
A.∠AOC= ∠BOC
B.∠AOC<∠AOB
C.∠AOC= ∠BOC 或∠AOC= 2∠BOC
D.∠AOC= ∠BOC 或∠AOC= 3∠BOC
D
)
A.∠AOC= ∠BOC
B.∠AOC<∠AOB
C.∠AOC= ∠BOC 或∠AOC= 2∠BOC
D.∠AOC= ∠BOC 或∠AOC= 3∠BOC
答案:
D
8 易错题 (2024 徐州沛县月考)已知 OC 是∠AOB 的平分线,∠BOD= $\frac{1}{3}$∠COD,OE 平分∠COD,设∠AOB= α,则∠BOE 等于(
A.$\frac{5}{16}$α 或 $\frac{1}{8}$α
B.$\frac{5}{16}$α 或 $\frac{1}{6}$α
C.$\frac{1}{8}$α 或 $\frac{1}{6}$α
D.$\frac{1}{6}$α
A
)A.$\frac{5}{16}$α 或 $\frac{1}{8}$α
B.$\frac{5}{16}$α 或 $\frac{1}{6}$α
C.$\frac{1}{8}$α 或 $\frac{1}{6}$α
D.$\frac{1}{6}$α
答案:
A
9 (2024 南京玄武月考)如图,将三个同样的正方形的一个顶点重合放置,如果∠1= 45°,∠3= 30°,那么∠2 的度数是
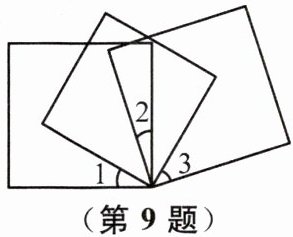
15°
.
答案:
15°
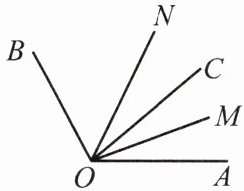
10 如图,已知∠AOB= 120°,OC 是∠AOB 内的一条射线,且∠AOC∶∠BOC= 1∶2.
(1)求∠AOC 和∠BOC 的度数;
(2)作射线 OM 平分∠AOC,在∠BOC 内作射线 ON,使得∠CON∶∠BON= 1∶3,求∠MON 的度数.
(1)求∠AOC 和∠BOC 的度数;
(2)作射线 OM 平分∠AOC,在∠BOC 内作射线 ON,使得∠CON∶∠BON= 1∶3,求∠MON 的度数.

答案:
(1)设∠AOC=α,则∠BOC=2α,因为∠AOB=120°,∠AOC+∠BOC=∠AOB,所以α+2α=120°,所以α=40°,所以∠AOC=40°,∠BOC=80°.
(2)因为OM平分∠AOC,所以∠MOC=$\frac{1}{2}$∠COA=$\frac{1}{2}$×40°=20°.因为∠CON:∠BON=1:3,所以∠NOC=$\frac{1}{4}$∠COB=$\frac{1}{4}$×80°=20°,所以∠MON=∠COM+∠CON=20°+20°=40°.
(1)设∠AOC=α,则∠BOC=2α,因为∠AOB=120°,∠AOC+∠BOC=∠AOB,所以α+2α=120°,所以α=40°,所以∠AOC=40°,∠BOC=80°.
(2)因为OM平分∠AOC,所以∠MOC=$\frac{1}{2}$∠COA=$\frac{1}{2}$×40°=20°.因为∠CON:∠BON=1:3,所以∠NOC=$\frac{1}{4}$∠COB=$\frac{1}{4}$×80°=20°,所以∠MON=∠COM+∠CON=20°+20°=40°.
11 如图,将一副标准三角板摆放在一起,∠DAB= m°.
(1)当 0<m<45 时,
①若 m= 20,则∠CAD=
②∠CAD 与∠BAE 的数量关系为
(2)当 0<m<120,且∠BAE= 6∠CAD 时,求 m 的值.
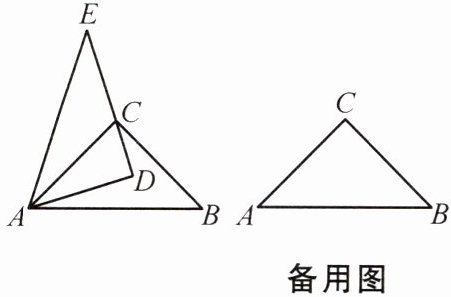
(1)当 0<m<45 时,
①若 m= 20,则∠CAD=
25°
,∠BAE= 80°
;②∠CAD 与∠BAE 的数量关系为
∠CAD+∠BAE=105°
;(2)当 0<m<120,且∠BAE= 6∠CAD 时,求 m 的值.
当0<m≤45时,由∠BAE=6∠CAD,得60+m=6(45 - m),解得m=30;当45<m<120时,由∠BAE=6∠CAD,得m+60=6(m - 45),解得m=66.综上,m的值为30或66.

答案:
(1)①25° 80° ②∠CAD+∠BAE=105°
(2)当0<m≤45时,由∠BAE=6∠CAD,得60+m=6(45 - m),解得m=30;当45<m<120时,由∠BAE=6∠CAD,得m+60=6(m - 45),解得m=66.综上,m的值为30或66.
(1)①25° 80° ②∠CAD+∠BAE=105°
(2)当0<m≤45时,由∠BAE=6∠CAD,得60+m=6(45 - m),解得m=30;当45<m<120时,由∠BAE=6∠CAD,得m+60=6(m - 45),解得m=66.综上,m的值为30或66.
查看更多完整答案,请扫码查看


