《2025年小学学霸作业本六年级数学上册苏教版江苏专版》

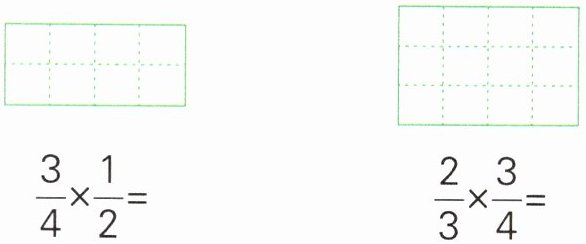
1. 先涂一涂,再计算。
$ \frac { 3 } { 4 } × \frac { 1 } { 2 } = $$\frac{3}{8}$
$ \frac { 2 } { 3 } × \frac { 3 } { 4 } = $$\frac{1}{2}$

答案： 本题可根据分数乘分数的意义进行涂一涂，再根据分数乘分数的计算法则进行计算。
1. 计算$\frac{3}{4}×\frac{1}{2}$
涂一涂：
把长方形看作单位“$1$”，先平均分成$4$份，取其中的$3$份涂上一种颜色（比如红色），表示$\frac{3}{4}$；再把这$\frac{3}{4}$平均分成$2$份，取其中的$1$份涂上另一种颜色（比如蓝色），这部分就表示$\frac{3}{4}$的$\frac{1}{2}$。
计算：
根据分数乘分数的计算法则：分数乘分数，用分子相乘的积做分子，分母相乘的积做分母。
$\frac{3}{4}×\frac{1}{2}=\frac{3×1}{4×2}=\frac{3}{8}$
2. 计算$\frac{2}{3}×\frac{3}{4}$
涂一涂：
把长方形看作单位“$1$”，先平均分成$3$份，取其中的$2$份涂上一种颜色（比如红色），表示$\frac{2}{3}$；再把这$\frac{2}{3}$平均分成$4$份，取其中的$3$份涂上另一种颜色（比如蓝色），这部分就表示$\frac{2}{3}$的$\frac{3}{4}$。
计算：
根据分数乘分数的计算法则：分数乘分数，用分子相乘的积做分子，分母相乘的积做分母，能约分的先约分再计算。
$\frac{2}{3}×\frac{3}{4}=\frac{2×3}{3×4}=\frac{1}{2}$
综上，答案依次为$\frac{3}{8}$；$\frac{1}{2}$。图略（按照上述涂一涂的描述进行涂色即可）。

2. 填空。
(1)$$ \frac { 5 } { 6 } × \frac { 2 } { 3 } = \frac { ( 5 ) × ( 2 ) } { ( 6 ) × ( 3 ) } = ( $\frac {5}{9}$ ) $(2)$$ \frac { 3 } { 5 } × \frac { 10 } { 9 } = \frac { ( 3 ) × ( 10 ) } { ( 5 ) × ( 9 ) } = ( $\frac {2}{3}$ ) $
(3)(名校期末真题)$$ \frac { 3 } { 4 } $$米的$$ \frac { 1 } { 2 } $$是( $\frac {3}{8}$ )米,$$ \frac { 4 } { 9 } $$千克的$$ \frac { 3 } { 8 } $$是( $\frac {1}{6}$ )千克。

答案： 解析：
题目考查的是分数乘分数的计算方法，以及分数乘法在实际问题中的应用。
对于分数乘分数，我们需要将两个分数的分子相乘作为新的分子，两个分数的分母相乘作为新的分母。
对于实际问题中的分数乘法，我们需要将给定的数与分数相乘，得出结果。
答案：
(1) $\frac { 5 } { 6 } × \frac { 2 } { 3 } = \frac { 5 × 2 } { 6 × 3 } = \frac { 5 } { 9 }$（或 $\frac {10}{18}$化简得$\frac {5}{9}$）
所以填空处应填：5；2；6；3；$\frac {5}{9}$
(2) $\frac { 3 } { 5 } × \frac { 10 } { 9 } = \frac { 3 × 10 } { 5 × 9 } = \frac { 2 } { 3 }$（或 $\frac {30}{45}$化简得$\frac {2}{3}$）
所以填空处应填：3；10；5；9；$\frac {2}{3}$
(3) $\frac { 3 } { 4 } × \frac { 1 } { 2 } = \frac { 3 } { 8 }$（米）
$\frac { 4 } { 9 } × \frac { 3 } { 8 } = \frac { 1 } { 6 }$（千克）
所以填空处应填：$\frac {3}{8}$；$\frac {1}{6}$

(1)$$ 4 × \frac { 8 } { 9 } = \frac { 4 × \bcancel { 8 } } { \bcancel { 1 } × 9 } = \frac { 2 } { 9 } $$ (×)
改正：$4×\frac{8}{9}=\frac{4×8}{9}=\frac{32}{9}$
(2)$$ \frac { 8 } { 15 } × \frac { 4 } { 5 } = \frac { \bcancel { 8 } ^ { 2 } } { \bcancel { 15 } _ { 3 } } × \frac { \bcancel { 4 } ^ { 1 } } { \bcancel { 5 } _ { 1 } } = \frac { 2 } { 3 } $$ (×)
改正：$\frac{8}{15}×\frac{4}{5}=\frac{8×4}{15×5}=\frac{32}{75}$

答案： 解析：本题考查的是分数乘法的计算法则，即分数乘分数，用分子相乘的积做分子，分母相乘的积做分母，能约分的先约分再计算。
(1)原计算过程错误，因为$4×\frac{8}{9}$的计算中，4应与分母9直接相乘，而不是与分子8相约分。
改正后的计算过程为：
$4×\frac{8}{9}=\frac{4×8}{9}=\frac{32}{9}$，
答案为：$×$，$\frac{32}{9}$。
(2)原计算过程错误，因为$\frac{8}{15}×\frac{4}{5}$的计算中，分子8与4相乘得到32，分母15与5相乘得到75，不能直接将8和15，4和5约分。
改正后的计算过程为：
$\frac{8}{15}×\frac{4}{5}=\frac{8×4}{15×5}=\frac{32}{75}$，
答案为：$×$，$\frac{32}{75}$。

4. 计算小能手。
$ \frac { 1 } { 5 } × \frac { 3 } { 4 } = $$\frac{3}{20}$
$ \frac { 3 } { 7 } × \frac { 1 } { 3 } = $$\frac{1}{7}$
$ \frac { 8 } { 3 } × \frac { 7 } { 12 } = $$\frac{14}{9}$
$ \frac { 17 } { 20 } × \frac { 15 } { 34 } = $$\frac{3}{8}$
$ \frac { 9 } { 10 } × \frac { 4 } { 15 } = $$\frac{6}{25}$
$ \frac { 13 } { 18 } × \frac { 2 } { 39 } = $$\frac{1}{27}$

答案： 解析：本题考查分数乘分数的计算方法。分数乘分数，用分子相乘的积做分子，分母相乘的积做分母，能约分的先约分再计算。
答案：
$\frac{1}{5} × \frac{3}{4} = \frac{3}{20}$
$\frac{3}{7} × \frac{1}{3} = \frac{1}{7}$
$\frac{8}{3} × \frac{7}{12} = \frac{14}{9}$
$\frac{17}{20} × \frac{15}{34} = \frac{3}{8}$
$\frac{9}{10} × \frac{4}{15} = \frac{6}{25}$
$\frac{13}{18} × \frac{2}{39} = \frac{1}{27}$

5. 牛奶是最古老的天然饮料之一,被誉为“白色血液”。妈妈买了一盒$$ \frac { 10 } { 9 } $$升的牛奶,早饭时小军喝了$$ \frac { 1 } { 3 } $$,小军喝了多少升？

答案： 解析：本题考查分数乘法的实际应用。要求小军喝了多少升牛奶，需要用妈妈买的牛奶总量乘以小军喝掉的比例。
答案：$\frac { 10 } { 9 }×\frac { 1 } { 3 }=\frac { 10 } { 27 }$(升)
答：小军喝了$\frac { 10 } { 27 }$升牛奶。

6. 一台收割机1小时可以收割一块麦田的$$ \frac { 5 } { 8 } $$,它$$ \frac { 1 } { 3 } $$小时可以收割这块麦田的几分之几？$$ \frac { 4 } { 5 } $$小时呢？

答案： 解析：本题考查分数乘法的应用。
求一个数的几分之几是多少用乘法计算。
首先，我们已知一台收割机1小时可以收割一块麦田的$\frac{5}{8}$。
接下来，我们要计算它$\frac{1}{3}$小时可以收割这块麦田的几分之几。
我们可以将1小时的工作量$\frac{5}{8}$乘以$\frac{1}{3}$，即：
$\frac{5}{8} × \frac{1}{3} = \frac{5 × 1}{8 × 3} = \frac{5}{24}$
所以，收割机$\frac{1}{3}$小时可以收割这块麦田的$\frac{5}{24}$。
然后，我们计算收割机$\frac{4}{5}$小时可以收割这块麦田的几分之几。
同样地，我们将1小时的工作量$\frac{5}{8}$乘以$\frac{4}{5}$，即：
$\frac{5}{8} × \frac{4}{5} = \frac{5 × 4}{8 × 5} = \frac{20}{40} = \frac{1}{2}$
所以，收割机$\frac{4}{5}$小时可以收割这块麦田的$\frac{1}{2}$。
答案：$\frac{5}{24}$，$\frac{1}{2}$。

7. 一盒糖果里有水果糖和牛奶糖共$ \frac { 9 } { 5 } $千克,小辰从水果糖和牛奶糖里各拿出$ \frac { 1 } { 3 } $送给小可,小辰共送给小可$\frac{3}{5}$千克糖果？

答案： 本题可根据乘法分配律的逆运算来求解小辰送给小可的糖果重量。
步骤一：分析已知条件
已知水果糖和牛奶糖总重量为$\frac{9}{5}$千克，小辰从水果糖和牛奶糖里各拿出$\frac{1}{3}$送给小可。
步骤二：计算送给小可的糖果重量
设水果糖重量为$a$千克，牛奶糖重量为$b$千克，则$a + b=\frac{9}{5}$千克。
小辰送给小可的水果糖重量为$\frac{1}{3}a$千克，送给小可的牛奶糖重量为$\frac{1}{3}b$千克。
那么小辰送给小可的糖果总重量为$\frac{1}{3}a+\frac{1}{3}b$千克。
根据乘法分配律的逆运算$ac + bc=(a + b)c$（其中$c$为相同因数），可得：
$\frac{1}{3}a+\frac{1}{3}b=\frac{1}{3}(a + b)$
将$a + b=\frac{9}{5}$代入上式，可得：
$\frac{1}{3}×\frac{9}{5}$
根据分数乘法法则：分数乘分数，用分子相乘的积做分子，分母相乘的积做分母，可得：
$\frac{1×9}{3×5}=\frac{9}{15}=\frac{3}{5}$（千克）
综上，小辰共送给小可$\boldsymbol{\frac{3}{5}}$千克糖果。

$ \frac { 1 } { 6 } × \frac { 3 } { 4 } = $
$ \frac { 5 } { 12 } × \frac { 9 } { 25 } = $
$ \frac { 8 } { 3 } × 9 = $
$ \frac { 2 } { 3 } × \frac { 3 } { 8 } = $
$ \frac { 7 } { 5 } × \frac { 3 } { 14 } = $

答案： 解析：本题主要考查分数乘法的运算。在分数乘法中，应注意分子与分子相乘，分母与分母相乘，之后进行必要的化简。
答案：
$\frac{1}{6} × \frac{3}{4} = \frac{1 × 3}{6 × 4} = \frac{3}{24} = \frac{1}{8}$
$\frac{5}{12} × \frac{9}{25} = \frac{5 × 9}{12 × 25} = \frac{45}{300} = \frac{3}{20}$
$\frac{8}{3} × 9 = \frac{8 × 9}{3} = \frac{72}{3} = 24$
$\frac{2}{3} × \frac{3}{8} = \frac{2 × 3}{3 × 8} = \frac{6}{24} = \frac{1}{4}$
$\frac{7}{5} × \frac{3}{14} = \frac{7 × 3}{5 × 14} = \frac{21}{70} = \frac{3}{10}$