《2025年1课3练单元达标测试八年级物理上册苏科版》

14 学过长度测量后,小芳想测量小钢珠的直径.她的做法：在水平桌面上,将 10 个相同的小钢珠紧密排列成一排,用两个三角板在两端挡住,测出 10 个小钢珠的总长度,即可算出小钢珠的直径,如图所示.

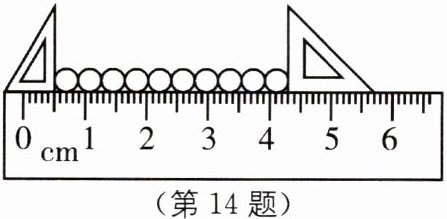
(1)实验中所用刻度尺的分度值是______,小钢珠的直径为______.
(2)小芳同学测量时的不足之处是______.
(3)用这种方法测小钢珠的直径,要使测得的数值更接近真实值,你的建议是______.
(4)这种测量方法称之为累积法,间接进行测量,体现了转换的物理思想.利用这种思想还可以测量______.(答案合理即可)

答案： 14.
(1)1mm 3.80mm
(2)不能保证两三角板之间的距离为10个钢珠的直径和
(3)找一个内径比小钢珠直径稍大的玻璃管,将小钢珠放入玻璃管内测量
(4)一张纸的厚度 [解析]
(1)图中刻度尺的1cm之间有10个小格,每小格代表0.1cm=1mm,所以刻度尺的分度值是1mm;左边三角板的直角边与0.5cm刻度线对齐,读作0.50cm,右边三角板的直角边与4.3cm刻度线对齐,读作4.30cm,所以10个小钢珠的直径和为L=4.30cm-0.50cm=3.80cm,一个小钢珠的直径为d= $\frac{1}{10}$×3.80cm=0.380cm=3.80mm.
(2)在桌面上将小钢珠排成一排后,因为两三角板在两端所挡住的位置不一定是小钢珠球心连线所在直线,不能保证两三角板之间的距离为10个钢珠的直径和.
(3)累积法测小钢珠的直径,要使测得的数值更接近真实值,可以找一个内径比小钢珠直径稍大的玻璃管,将小钢珠放入玻璃管内测量,这样可以使得10个小钢珠的球心在一条直线上.
(4)累积法测量的应用很多,如测量一张纸的厚度、测量细铁丝的直径等.关键提醒
(1)在桌面上将小钢珠排成一排后,两三角板所挡住的位置不能确定是钢球球心连线所在直线;
(2)累积法测小钢珠的直径,要使测得的数值更接近真实值,应设法使小钢珠的球心在一条直线上;
(3)利用积少成多,测多求少的方法来间接地测量,可以减小误差.

15 中考新考法 开放性实验设计 小羽同学通过阅读《伽利略对摆动的研究》内容,了解到“不论摆动的幅度大些还是小些,完成一次摆动的时间是一样的”.小羽用一条长绳的一端系一个螺母做成了一个摆,如图所示.想用秒表测出它摆动一个来回所用的时间(周期).(注：摆长 L 是指绳子固定点 O 到重物重心的距离)

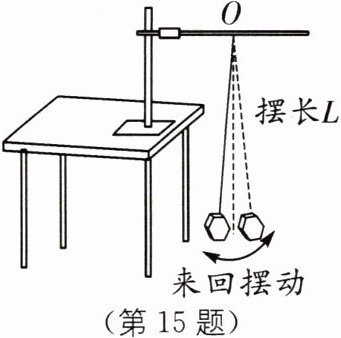
小羽发现它摆动一个来回所用的时间比较短,用秒表难以测准,只利用现有器材,想测得更准确的方法是______.

答案： 15. 用秒表测出这个摆摆动N(20或30等)个来回所用的时间t,然后用T= $\frac{t}{N}$求出摆动一个来回所用的时间 [解析]摆动一个来回所用的时间比较短,为了减小时间的测量误差,可以用秒表测出这个摆摆动N(20或30等)个来回所用的时间t,然后用T= $\frac{t}{N}$求出摆动一个来回所用的时间.素养考向 本题是探究单摆摆动周期的实验,考查了采用累积法减小误差的测量方法.

16 想要测量北京到上海的铁路线的长度,小明采用如下步骤：
A. 用 L 结合地图比例尺即可算出北京到上海两地的铁路线长
B. 取下棉线,将棉线轻轻拉直,用刻度尺测出两记号间的长度 L
C. 找一张铁路交通地图,找到北京到上海的铁路线
D. 把软棉线(无弹性)与所选的铁路线重合,在北京和上海两地处用红笔在棉线上做记号
(1)正确的操作顺序应该是______.
(2)能否用有弹性的橡皮筋代替软棉线？______(填“能”或“不能”).
(3)测量长度时先观察刻度尺的______、______、______,刻度尺要与拉直的棉线______(填“平行”或“垂直”),读数时要估读到______的下一位.

答案： 16.
(1)C、D、B、A
(2)不能
(3)量程 零刻度线 分度值 平行 分度值 [解析]
(1)测量北京到上海的铁路线的长度时,应用一根无弹性的棉线和曲线重合来测量,轻轻拉直棉线后再用刻度尺测量,再根据比例尺计算出北京到上海两地的铁路线长,故正确的操作顺序应该是C、D、B、A.
(2)有弹性的橡皮筋长度不稳定,拉直后长度会变长,会影响测量结果的准确性,所以不能用它代替软棉线.
(3)测量长度时,首先要了解刻度尺的量程、零刻度线、分度值;使用时,让刻度尺有刻度的一面紧贴被测部分,刻度尺要与拉直的棉线平行,读数时结果要估读到分度值的下一位.

17 常用的卷筒纸是紧密地绕成筒状的,如图所示,小明同学想在不把纸放开的前提下,测量整卷纸的长度.他设计的方案如下：

(1)将同类纸折叠 n 层,用刻度尺测得总厚度为 d,则单层纸的厚度为______.设纸的宽度为 s,整卷纸的长为 L,则纸筒的体积可表示为 $ V = $______.
(2)用刻度尺测得纸筒的外半径为 R,内半径为 r,则纸筒的体积可表示为______.
(3)由以上两式可整理得整卷纸的长度为______.
(4)步骤(1)中测量单层纸的厚度时求平均值的目的是______.

答案： 17.
(1) $\frac{d}{n}$ $\frac{Lsd}{n}$
(2)πs($R^2$-$r^2$)
(3) $\frac{nπ(R^2-r^2)}{d}$
(4)减小误差 [解析]
(1)同类纸折叠n层,用刻度尺测得总厚度为d,则单层纸的厚度是 $\frac{d}{n}$;纸的宽度为s,整卷纸的长度为L,则纸筒的体积可表示为V= $\frac{Lsd}{n}$.
(2)不可能把纸拉直再测量长度,但卷成筒状的纸的横截面积是由纸的厚度和长度叠加而成的,则测出横截面积的大小为π($R^2$-$r^2$),故纸筒的体积是V=πs($R^2$-$r^2$).
(3)由题意可得 $\frac{Lsd}{n}$=πs($R^2$-$r^2$),解得L= $\frac{nπ(R^2-r^2)}{d}$.
(4)测量厚度时,需要多次测量,取平均值,其目的是减小误差.名师点评 本题考查长度测量的特殊方法,注意合理利用累积法测量,同时考虑减小测量误差的方法.