《2025年1课3练单元达标测试七年级数学上册人教版》

1. 有理数乘除混合运算步骤：
(1)将除法转化为____,除数转化为____；
(2)先确定积的____,再把绝对值____；
(3)运用乘法的____,简化计算；
(4)求出最简结果。

答案： 1.
(1)乘法 倒数
(2)符号 相乘
(3)运算律

2. 有理数的加减乘除混合运算：
(1)无括号：先算____,后算____；
(2)有括号：先算____里面的；
(3)同级运算,按从左到右的顺序进行。

答案： 2.
(1)乘除 加减
(2)括号

3. 计算$(-2)÷(-\frac {1}{16})÷(-4)$得( )。

A.-8
B.8
C.$-\frac {1}{4}$
D.$-\frac {1}{32}$

答案： 3.A

4. 计算：$24÷(-4)×(-3)$的结果是( )。

A.-18
B.18
C.-2
D.2

答案： 4.B

5. 在-1,2,-3,0,5这五个数中,任取两个相除,其中商最小的是____。

答案： 5.-5

6. 提分优练 计算：
(1)$(-1.5)×\frac {4}{5}÷(-\frac {2}{5})×\frac {1}{4}$；
(2)$-2\frac {13}{16}÷(\frac {3}{4}×\frac {9}{8})$；
(3)$(-3\frac {1}{3})÷2\frac {4}{5}÷(-3\frac {1}{8})$。

答案： 6.
(1)原式$=\frac{3}{2}×\frac{4}{5}×\frac{5}{2}×\frac{1}{4}=\frac{3}{4}.$
(2)原式$=(-\frac{45}{16})÷\frac{27}{32}=(-\frac{45}{16})×\frac{32}{27}=-3\frac{1}{3}.$
(3)原式$=\frac{10}{3}×\frac{5}{14}×\frac{8}{25}=\frac{8}{21}.$

1. 乘方的定义：
一般地,$n个相同的乘数a$相乘,即$\underbrace{a\cdot a…\cdot \cdot a}_{n个}$,记作$a^{n}$,读作“$a的n$次方”.
求$n$个相同____的积的运算,叫作乘方.

答案： 乘数

2. 乘方的意义：
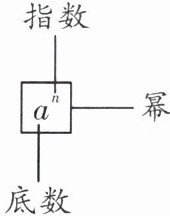
乘方的结果叫作幂,在$a^{n}$中,$a$叫作____,$n$叫作____,当$a^{n}看作a的n$次方的结果时,也可读作“$a的n$次幂”.

答案： 底数　指数

3. 有理数乘方运算的符号规律：
(1)负数的奇次幂是____数；负数的偶次幂是____数；
(2)正数的任何次幂都是____数；
(3)$0$的任何正整数次幂都是____.

答案：
(1)负　正　
(2)正　
(3)0