《2025年1课3练单元达标测试七年级数学上册人教版》

1 (2024·江西南昌期末)已知$a= -3$,则代数式$a^{2}+1$的值为(D).
A.-5
B.7
C.-8
D.10

答案： D

当$x= -1,y= 3$时,代数式$x^{3}-2y$的值为(A).
A.-7
B.-5
C.4
D.7

答案： A

如图,当输入$x$的值为-1时,输出的结果为(B).
A.-1
B.11
C.2
D.43

答案： B [解析]当输入x的值为-1时,-2x+1=-2×(-1)+1=3＜10,
∴需重新输入x的值为3,
∴-2x+1=-2×3+1=-5＜10,
∴需重新输入x的值为-5,
∴-2x+1=-2×(-5)+1=10+1=11＞10,
∴输出的结果为11.故选B.

4 (2024·苏州中考)若$a= b+2$,则$(b-a)^{2}= $4.

答案： 4 [解析]
∵a=b+2,
∴b-a=-2,
∴(b-a)²=(-2)²=4.

5 教材 P79 例 2·变式 当$a= 2,b= -1,c= -3$时,求下列各代数式的值：
(1)$b^{2}-4ac$;
(2)$a^{2}-2ab+b^{2}$.

答案：
(1)当a=2,b=-1,c=-3时,原式=(-1)²-4×2×(-3)=1+24=25.
(2)当a=2,b=-1时,原式=2²-2×2×(-1)+(-1)²=4+4+1=9.

6 (2024·北京顺义区期末)自行车的链条由一个个小的链节组成,如图,每个链节的长度为 2.5 cm,链节与链节之间交叉重叠部分的圆的直径为 0.8 cm.

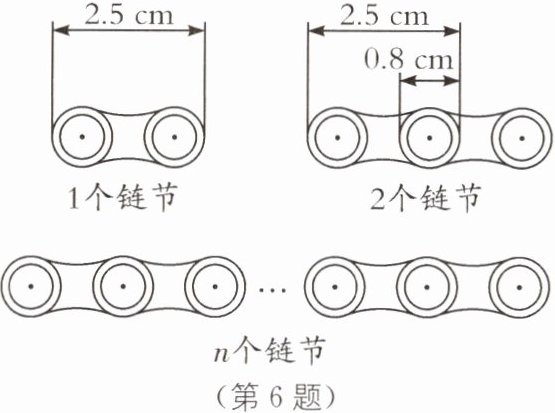
则$n$个链节依次连在一起的长度是1.7n+0.8cm,如果一辆自行车的链条(安装前)由 60 个这样的链节组成,那么这辆自行车的链条(安装后)的总长度是102cm.

答案： (1.7n+0.8) 102 [解析]由题图,可得n个链节依次连在一起的长度是0.8+(2.5-0.8)n=(1.7n+0.8)cm.当n=60时,1.7×60+0.8=102.8(cm).当链条安装完后,总长度为102.8-0.8=102(cm).

7 如图,用小棒搭正方形,仔细观察图形,可以发现:搭一个正方形需要 4 根小棒,搭两个正方形需要 7 根小棒,搭三个正方形需要 10 根小棒…

(1)搭四个正方形需要13根小棒；
(2)按照图中方式继续搭下去,则搭$n$个正方形($n$是正整数)需要小棒的根数是3n+1；(用含$n$的代数式表示)
(3)求搭 48 个正方形需要多少根小棒.
当n=48时,3n+1=3×48+1=145(根).故搭48个正方形需要145根小棒.

答案：
(1)13
(2)3n+1
(3)当n=48时,3n+1=3×48+1=145(根).故搭48个正方形需要145根小棒.

8 (2024·广东江门蓬江区期末)若$x^{2}+3x= 2$,则 2023$+2x^{2}+6x$的值为(A).
A.2027
B.2026
C.2025
D.2024

答案： A [解析]
∵x²+3x=2,
∴2x²+6x=4,
∴2023+2x²+6x=2023+4=2027.故选A.