《2025年1课3练单元达标测试七年级数学上册人教版》

12 (2024·江西景德镇期末)用代数式表示“a的2倍与b的差的平方”,正确的是(C).
A.$ 2(a - b)^{2} $
B.$ 2a - b^{2} $
C.$ (2a - b)^{2} $
D.$ (a - 2b)^{2} $

答案： C

13 某工厂计划生产n个零件,原计划每天生产a个零件,实际每天比原计划多生产b个零件,则实际生产所用的天数比原计划少(D).
A.$ (\frac{n}{a}-\frac{n}{b}) $天
B.$ (\frac{n}{b}-\frac{n}{a}) $天
C.$ (\frac{n}{a + b}-\frac{n}{a}) $天
D.$ (\frac{n}{a}-\frac{n}{a + b}) $天

答案： D [解析]由题意,得原计划生产n个零件需要$\frac {n}{a}$天,实际生产n个零件需要$\frac {n}{a+b}$天,
∴实际生产所用的天数比原计划少$(\frac {n}{a}-\frac {n}{a+b})$天.故选D.

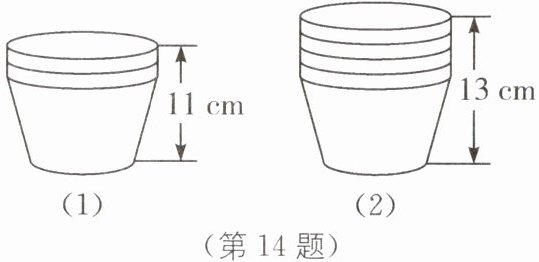
14 (2024·河北石家庄期末)小明在超市买回若干个相同的纸杯,他把纸杯整齐地叠放在一起.如图(1),3个纸杯的高度为11cm;如图(2),5个纸杯的高度为13cm.若把n个这样的纸杯叠放在一起,则高度为(B).


A.$ (n + 10) $cm
B.$ (n + 8) $cm
C.$ (2n + 5) $cm
D.$ (2n + 3) $cm

答案： B [解析]由题意,得每增加一个水杯,增加的高度是$(13-11)÷(5-3)=2÷2=1(cm)$,
∴把n个这样的杯子叠放在一起,高度为$11+(n-3)×1=11+n-3=(n+8)cm$.故选B.

15 (2024·镇江句容模拟)培根在《论学问》中说“阅读使人充实”.爱好阅读的小宁前年读了m本书,去年阅读数量是前年的2倍,则小宁去年阅读了2m本书.

答案： 2m

16 (2024·山东泰安期末)结合实际例子,代数式$ (1 - 25\%)a $可以解释为原计划生产a个零件,实际比计划减产25%,求实际生产多少个零件(答案不唯一).

答案： 原计划生产a个零件,实际比计划减产25%,求实际生产多少个零件(答案不唯一)

17 (2024·天津南开区期末)某个两位数,十位上的数为a,个位上的数为b,将其十位上的数与个位上的数交换位置,得到一个新的两位数,新两位数用式子表示为$10b+a$.

答案： $10b+a$ [解析]
∵十位数字为a,个位数字为b,将其十位上的数与个位上的数交换位置,得到一个新的两位数,
∴新的两位数的十位数字为b,个位数字为a,
∴这个新的两位数用代数式表示为$10b+a.$

18 (2024·湖南长沙期中)下列式子书写规范吗?若不规范,请将它们的规范写法填在横线处:
(1)$ a×20 $: 20a;(2)$ 1\frac{1}{3}x $: $\frac {4}{3}x$;
(3)$ -1mn $: -mn;(4)$ s÷ t $: $\frac {s}{t}$.

答案：
(1)20a
(2)$\frac {4}{3}x$
(3)-mn
(4)$\frac {s}{t}$

19 列出代数式.
(1)长方形的长为x,宽为y,则长方形的面积是多少?
(2)一台电视机原价a元,现按原价9折出售,那么这台电视机现在的售价是多少?
(3)某班总人数为m人,女生人数是男生人数的$ \frac{3}{5} $,那么该班男生有多少人?

答案：
(1)xy
(2)0.9a
(3)$\frac {5}{8}m$

20 教材 P73练习T4·变式 某学校要对如图所示的一块长方形空地进行绿化,长方形的长AB为a,宽BC为b,分别以A,B为圆心,BC长为半径作扇形,图中阴影部分种植草坪.用含有a,b的代数式表示种植草坪部分(阴影部分)的面积S.(结果保留π)

答案： 长方形的面积为ab,一个扇形的面积为$\frac {1}{4}πb^{2},$
∴$S=ab-2×\frac {1}{4}πb^{2}=ab-\frac {1}{2}πb^{2}.$