《2025年1课3练单元达标测试七年级数学上册人教版》

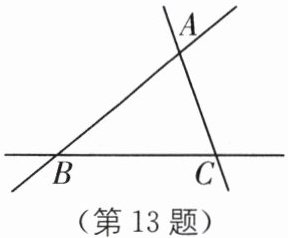
13. 直线$AB$,$BC$,$CA$的位置关系如图所示,则下列语句：①点$B在直线BC$上；②直线$AB经过点C$；③直线$AB$,$BC$,$CA$两两相交；④点$B是直线AB$,$BC$的交点.其中正确的有______.(只填写序号)

答案： ①③④

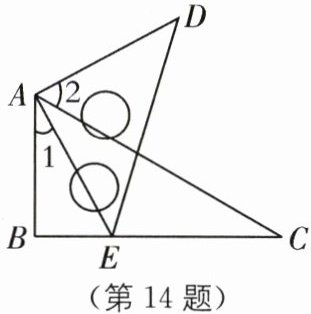
14.(2023·江苏泰州泰兴期末)如图,将一个三角板$60^{\circ}$角的顶点与另一个三角板的直角顶点重合.若$\angle 1 = 28^{\circ}48'$,则$\angle 2$的度数是______$^{\circ}$.

答案： 58.8 [解析]
∵∠BAC=60°，∠1=28°48'，
∴∠EAC=60° - 28°48'=31°12'.
∵∠EAD=90°，
∴∠2=90° - ∠EAC=90° - 31°12'=58°48'=58.8°.

15.(2024·浙江宁波期末)点$P在\angle MON$内部,则四个等式：①$\angle POM= \angle NCP$；②$\angle PON+\angle POM= \angle MON$；③$\angle MOP= \frac{1}{2}\angle MON$；④$\angle MON = 2\angle NOP$,其中能表示$OP是\angle MON$平分线的式子有______.(填写所有正确的序号)

答案： ①③④

16. 如图,$C是线段AB$上一点,$D是AC$的中点,点$M在CD$上,延长$AB到N$,使$BN = CM$.若$AB = 5$,$MN = 4$,则$DM$的长为______.

答案： $\frac{1}{2}$ [解析]设BN=CM=x，则AN=AB + BN=5 + x.
∴AM=AN - MN=5 + x - 4=1 + x，
∴AC=AM + CM=1 + x + x=1 + 2x.
∵D是AC的中点，
∴CD= $\frac{1}{2}$AC= $\frac{1}{2}$+x，
∴DM=CD - CM= $\frac{1}{2}$+x - x= $\frac{1}{2}$.

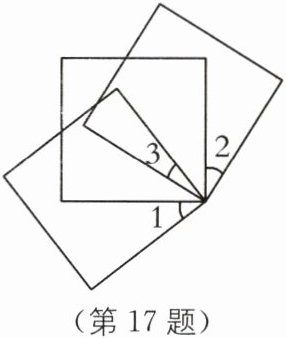
17.(2024·上海徐汇区期末)如图,将三个边长相同的正方形的一个顶点重合放置,已知$\angle 1 = 38^{\circ}$,$\angle 2 = 32^{\circ}$,则$\angle 3= $______度.

答案： 20

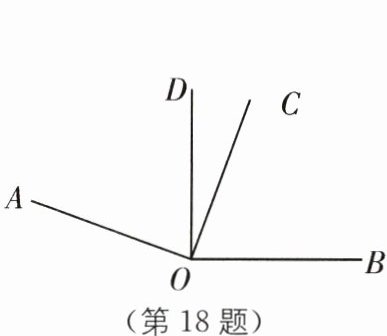
18.(2023·河南郑州二七区期中)如图,$\angle AOC和\angle BOD$都是直角,固定$\angle BOD$不动,将$\angle AOC绕点O$旋转,在旋转过程中,下列结论正确的有______.
①如果$\angle DOC = 20^{\circ}$,那么$\angle AOB = 160^{\circ}$；②$\angle DOC+\angle AOB$是定值；③如果$\angle DOC$变小,那么$\angle AOB$变大；④$\angle AOD= \angle BOC$.

答案： ①②③④ [解析]由题意，得∠AOC=∠BOD=90°，
∴∠AOD=∠AOC - ∠COD=90° - 20°=70°，
∴∠AOB=∠AOD + ∠BOD=70° + 90°=160°，故结论①正确；
∵∠DOC+∠AOB=(∠AOC - ∠AOD)+(∠AOD + ∠BOD)=∠AOC - ∠AOD + ∠AOD + ∠BOD=∠AOC + ∠BOD=90° + 90°=180°，故结论②正确；
∵由②结论，得∠DOC + ∠AOB=180°，
∴∠AOB=180° - ∠DOC，
∴如果∠DOC变小，那么∠AOB变大，故结论③正确；
∵∠AOC=∠AOD + ∠COD=90°，∠BOD=∠BOC + ∠COD=90°，
∴∠AOD=∠BOC，故结论④正确.综上所述，结论正确的有①②③④.