16. 已知关于x,y的多项式$x^2 + mx - 2y + n$与$nx^2 - 3x + 4y - 7$的差的值与字母x的取值无关,则n - m = ______.
答案:
4
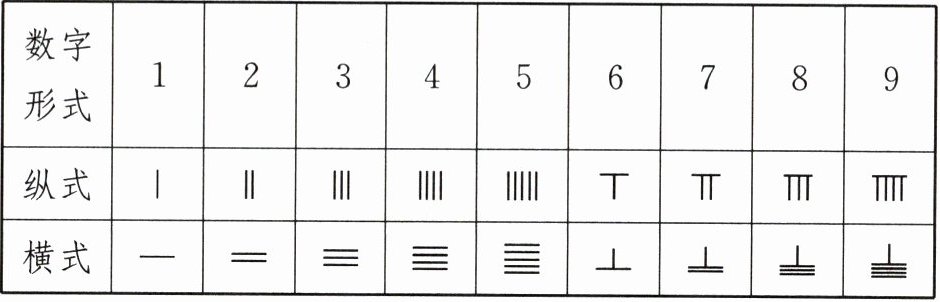
17. 传统文化 算筹 算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大的贡献. 在算筹计数法中,以“纵式”和“横式”两种方式来表示数字如下:
|数字形式|1|2|3|4|5|6|7|8|9|
|纵式| | || || || || || || ||
|横式|—|= |≡|≡|≡|⊥|⊥|⊥|⊥|
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空. 例如:⊥ = 6728,⊥= 6708,则 | ⊥ 表示的数是______.
|数字形式|1|2|3|4|5|6|7|8|9|
|纵式| | || || || || || || ||

|横式|—|= |≡|≡|≡|⊥|⊥|⊥|⊥|
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空. 例如:⊥ = 6728,⊥= 6708,则 | ⊥ 表示的数是______.
答案:
9.167
18. (2024·广东深圳福田区期末)已知a,b都是有理数,且满足$\frac{\vert a\vert}{a} + \frac{\vert b\vert}{b} = 0$,那么$\vert ab\vert + ab$ = ______.
答案:
0 [解析]
∵|a|a+|b|b=0,
∴a≠0,b≠0.当a>0时,|a|a+|b|b=0,
∴aa+|b|b=0,
∴1+|b|b=0,
∴|b|=-b,
∴b<0,
∴a,b异号,
∴|ab|+ab=-ab+ab=0;当a<0时,|a|a+|b|b=0,
∴-aa+|b|b=0,
∴-1+|b|b=0,
∴|b|=b,
∴b>0,
∴a,b异号,
∴|ab|+ab=-ab+ab=0.归纳总结 本题主要考查了有理数的乘法和绝对值的性质,解题关键是熟练掌握用分类讨论的思想判断a,b的符号.
∵|a|a+|b|b=0,
∴a≠0,b≠0.当a>0时,|a|a+|b|b=0,
∴aa+|b|b=0,
∴1+|b|b=0,
∴|b|=-b,
∴b<0,
∴a,b异号,
∴|ab|+ab=-ab+ab=0;当a<0时,|a|a+|b|b=0,
∴-aa+|b|b=0,
∴-1+|b|b=0,
∴|b|=b,
∴b>0,
∴a,b异号,
∴|ab|+ab=-ab+ab=0.归纳总结 本题主要考查了有理数的乘法和绝对值的性质,解题关键是熟练掌握用分类讨论的思想判断a,b的符号.
19. (8分)(2024·江苏南通期中)计算:
(1)-11 + 8 - (-9) + $\vert -3\vert$;
(2)-7 - 2×(-3) + (-6) + (-$\frac{1}{3}$);
(3)-48×(-$\frac{1}{6}$ + $\frac{3}{4}$ - $\frac{1}{24}$);
(4)-1^4 - $\frac{1}{6}$×[2 - (-3)^2].
(1)-11 + 8 - (-9) + $\vert -3\vert$;
(2)-7 - 2×(-3) + (-6) + (-$\frac{1}{3}$);
(3)-48×(-$\frac{1}{6}$ + $\frac{3}{4}$ - $\frac{1}{24}$);
(4)-1^4 - $\frac{1}{6}$×[2 - (-3)^2].
答案:
(1)-11 + 8 - (-9) + |-3|=-11+8+9+3=9;
(2)-7 - 2×(-3) + (-6) + (-13)=-7+6-6-13=-713;
(3)-48×(-16 + 34 - 124)=48×16 - 48×34 + 48×124=8 - 36 + 2=-26;
(4)-14 - 16×[2 - (-3)2]=-1 - 16×(2 - 9)=-1 + 76=16.
(1)-11 + 8 - (-9) + |-3|=-11+8+9+3=9;
(2)-7 - 2×(-3) + (-6) + (-13)=-7+6-6-13=-713;
(3)-48×(-16 + 34 - 124)=48×16 - 48×34 + 48×124=8 - 36 + 2=-26;
(4)-14 - 16×[2 - (-3)2]=-1 - 16×(2 - 9)=-1 + 76=16.
查看更多完整答案,请扫码查看


