第108页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
10(2024·浙江金华期末)下列图形绕虚线旋转一周,能形成圆锥的是(
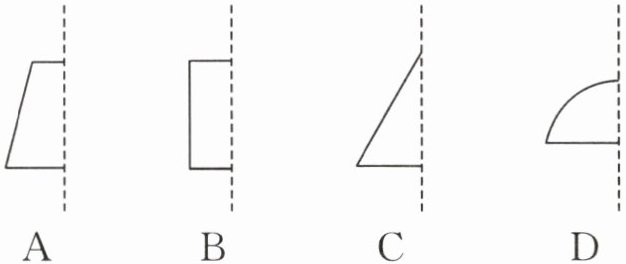
C
).
答案:
C
《雨不绝》是唐代诗人杜甫的作品,其中有诗句:鸣雨既过渐细微,映空摇飏如丝飞.诗中描写雨滴滴下来形成雨丝,用数学知识解释为
点动成线
.
答案:
点动成线
国扇文化有深厚的文化底蕴,历来中国有“制扇王国”之称.打开折扇时,随着扇骨的移动形成一个扇面,这种现象可以用数学原理解释为
线动成面
.
答案:
线动成面
(1)将此旋转门旋转一周,能形成的几何体是______
A. 点动成线
B. 线动成面
C. 面动成体
(2)求该旋转门旋转一周形成的几何体的体积.(边框及衔接处忽略不计,结果保留π)
圆柱
,这能说明的事实是______C
.(选择正确的一项填入)A. 点动成线
B. 线动成面
C. 面动成体
(2)求该旋转门旋转一周形成的几何体的体积.(边框及衔接处忽略不计,结果保留π)
该旋转门旋转一周形成的几何体是圆柱,体积为$\pi × 2^{2}× 3=12\pi (\unit{m^{3}})$.故形成的几何体的体积是$12\pi \ \unit{m^{3}}$.
答案:
(1)圆柱 C
(2)该旋转门旋转一周形成的几何体是圆柱,体积为$\pi × 2^{2}× 3=12\pi (\unit{m^{3}})$.故形成的几何体的体积是$12\pi \ \unit{m^{3}}$.
(1)圆柱 C
(2)该旋转门旋转一周形成的几何体是圆柱,体积为$\pi × 2^{2}× 3=12\pi (\unit{m^{3}})$.故形成的几何体的体积是$12\pi \ \unit{m^{3}}$.
14(2024·山东青岛期末)分别以直角梯形(如图所示)的下底和上底为轴,将梯形旋转一周得到 A,B 两个立体图形.则 A,B 两个立体图形的体积之比是(
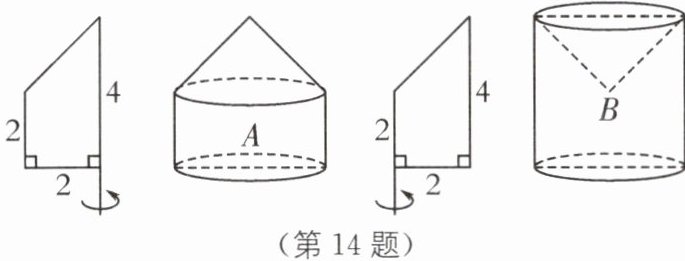
A.1:1
B.2:1
C.4:5
D.5:4
C
).
A.1:1
B.2:1
C.4:5
D.5:4
答案:
C [解析]几何体A的体积为$\pi × 2^{2}× 2+\frac{1}{3}\pi × 2^{2}× (4 - 2)=8\pi +\frac{8\pi }{3}=\frac{32\pi }{3}$;几何体B的体积为$\pi × 2^{2}× 4-\frac{1}{3}\pi × 2^{2}× (4 - 2)=16\pi -\frac{8\pi }{3}=\frac{40\pi }{3}$,所以A,B两个立体图形的体积之比是4:5.故选C.
15(2023·山东枣庄滕州期末)把一个长方形绕它的一条边所在的直线旋转一周能得到一个圆柱,那么把一个长为 4 cm、宽为 3 cm 的长方形绕它的一条边所在的直线旋转一周后,得到的圆柱的体积为
$36\pi \ \unit{cm^{3}}$或$48\pi \ \unit{cm^{3}}$
.(结果保留π)
答案:
$36\pi \ \unit{cm^{3}}$或$48\pi \ \unit{cm^{3}}$
16(2024·江苏无锡宜兴期中)如图(1),把一张长 8 厘米、宽 4 厘米的长方形纸板分成甲、乙两个相同的直角三角形.(π取 3.14)
(1)将甲三角形绕轴(如图(2))旋转一周,可以形成一个怎样的几何体?它的体积是多少立方厘米?
(2)将乙三角形绕轴(如图(3))旋转一周形成一个几何体,求该几何体的体积.
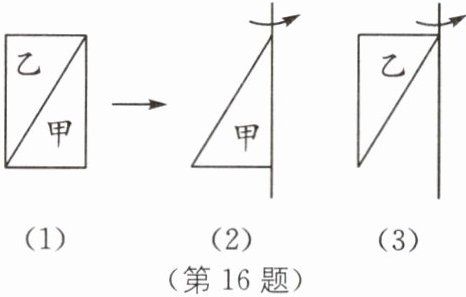
(1)将甲三角形绕轴(如图(2))旋转一周,可以形成一个怎样的几何体?它的体积是多少立方厘米?
(2)将乙三角形绕轴(如图(3))旋转一周形成一个几何体,求该几何体的体积.

答案:
(1)根据题干分析,可得以其中一个直角三角形较长的直角边所在直线为轴,将纸板快速转动,可以形成一个圆锥,它的体积是$\frac{1}{3}× 3.14× 4^{2}× 8=3.14× \frac{128}{3}\approx 134$(立方厘米).
(2)根据题干分析,可得乙三角形旋转一周,可以形成一个空心的圆柱,体积为$3.14× 4^{2}× 8-\frac{1}{3}× 3.14× 4^{2}× 8=3.14× 128-3.14× \frac{128}{3}\approx 268$(立方厘米).
(1)根据题干分析,可得以其中一个直角三角形较长的直角边所在直线为轴,将纸板快速转动,可以形成一个圆锥,它的体积是$\frac{1}{3}× 3.14× 4^{2}× 8=3.14× \frac{128}{3}\approx 134$(立方厘米).
(2)根据题干分析,可得乙三角形旋转一周,可以形成一个空心的圆柱,体积为$3.14× 4^{2}× 8-\frac{1}{3}× 3.14× 4^{2}× 8=3.14× 128-3.14× \frac{128}{3}\approx 268$(立方厘米).
查看更多完整答案,请扫码查看


