第102页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
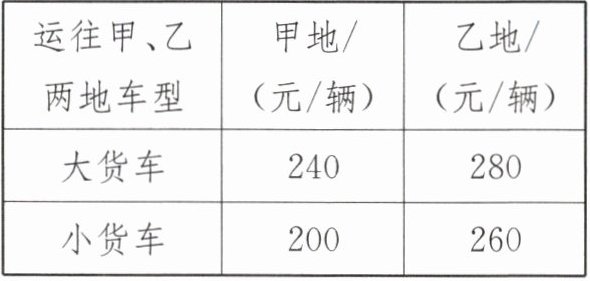
13 现要把160吨物资运往甲、乙两地,用大、小两种货车共15辆,恰好能一次性运完这批物资,已知这两种货车的载重量分别为12吨/辆和8吨/辆,运往甲、乙两地的运费如表:
|运往甲、乙两地车型|甲地/(元/辆)|乙地/(元/辆)|
|大货车|240|280|
|小货车|200|260|
(1)求这两种货车各用多少辆;
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,请直接写出用含a的式子表示运往甲、乙两地的总运费;
(3)在(2)的条件下,若运往乙地的物资为60吨,请直接写出安排前往甲地的大货车辆数,并直接写出此时的总运费.
|运往甲、乙两地车型|甲地/(元/辆)|乙地/(元/辆)|
|大货车|240|280|
|小货车|200|260|

(1)求这两种货车各用多少辆;
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,请直接写出用含a的式子表示运往甲、乙两地的总运费;
(3)在(2)的条件下,若运往乙地的物资为60吨,请直接写出安排前往甲地的大货车辆数,并直接写出此时的总运费.
答案:
(1)设大货车用x辆,则小货车用(15−x)辆,
由题意,得12x+8(15−x)=160,
解得x=10,
∴15−x=5(辆).
故大货车用10辆,小货车用5辆.
(2)运往甲、乙两地的总运费为240a+200(9−a)+280(10−a)+260[5−(9−a)]=(20a+3560)元.
(3)由题意,得12(10−a)+8(a−4)=60,
解得a=7,
∴20×7+3560=3700(元),
故安排前往甲地的大货车为7辆,此时的总费用为3700元.
(1)设大货车用x辆,则小货车用(15−x)辆,
由题意,得12x+8(15−x)=160,
解得x=10,
∴15−x=5(辆).
故大货车用10辆,小货车用5辆.
(2)运往甲、乙两地的总运费为240a+200(9−a)+280(10−a)+260[5−(9−a)]=(20a+3560)元.
(3)由题意,得12(10−a)+8(a−4)=60,
解得a=7,
∴20×7+3560=3700(元),
故安排前往甲地的大货车为7辆,此时的总费用为3700元.
14 (2024·江苏镇江丹阳期末)数轴上A,B两点对应的数分别是a,b,a,b满足$(a-8)^2+$|b+4|= 0.若有一动点P从数轴上点A出发,以每秒3个单位长度的速度沿数轴向点B匀速运动,动点Q从点B同时出发,以每秒2个单位长度的速度沿着数轴向点A匀速运动,规定其中一个动点到达终点时,另一个动点也随之停止运动.设运动时间为t秒.
(1)a= ,b= ,并在如图所示的数轴上面标出A,B两点;

(2)①当t= 1时,数轴上点P所表示的数是 ,点Q所表示的数是 ;
②问:点P运动多少秒时,与点Q相距3个单位长度?
(1)a= ,b= ,并在如图所示的数轴上面标出A,B两点;

(2)①当t= 1时,数轴上点P所表示的数是 ,点Q所表示的数是 ;
②问:点P运动多少秒时,与点Q相距3个单位长度?
答案:
(1)8 −4 [解析]
∵(a−8)²+|b+4|=0,
∴a−8=0,b+4=0,
∴a=8,b=−4.
在数轴上面标出A,B两点,如图:

(2)①5 −2
②运动时间为t秒,根据P,Q的运动,则AP=3t,
BQ=2t,AB=8−(−4)=12.
分两种情况:
当点P在点Q的右侧时,2t+3t=12−3,
∴t=$\frac{9}{5}$;当点P在点Q的左侧时,2t+3t=12+3,
∴t=3.故点P运动$\frac{9}{5}$秒或3秒时与点Q相距3个单位长度.
(1)8 −4 [解析]
∵(a−8)²+|b+4|=0,
∴a−8=0,b+4=0,
∴a=8,b=−4.
在数轴上面标出A,B两点,如图:

(2)①5 −2
②运动时间为t秒,根据P,Q的运动,则AP=3t,
BQ=2t,AB=8−(−4)=12.
分两种情况:
当点P在点Q的右侧时,2t+3t=12−3,
∴t=$\frac{9}{5}$;当点P在点Q的左侧时,2t+3t=12+3,
∴t=3.故点P运动$\frac{9}{5}$秒或3秒时与点Q相距3个单位长度.
查看更多完整答案,请扫码查看


