《2025年学霸甘肃少年儿童出版社四年级数学上册苏教版》

5. 推导探究 乐乐将算式“42×36-15×6”中的“5”漏写了,结果与正确答案相差多少?
(1)我是这样想的：“42×36”不变,“15×6”的“5”漏写了,变成“1×6”,也就是原来从“42×36”里减去15个 6,现在变成减去1个 6,相差了14个 6,也就是差了84。
(2)如果将“15”的“1”漏写了,结果会相差10个 6,也就是差了60。
(3)想一想,填一填。
625÷25+34×8= 625÷25+4×8+30×8
625÷25-34×8= 625÷25-3×8-31×8

答案：
(1)15 1 14 84
(2)10 60
(3)+ 30 - 31
提示:
(1)由题意可知,由15个6变成1个6,相差了15 - 1=14(个)6,即相差了14×6=84。
(2)由15个6变成5个6,相差了15 - 5=10(个)6,即相差了10×6=60。
(3)34个8变成4个8,相差了34 - 4=30(个)8,即再加上30×8即可;34个8变成3个8,相差了34 - 3=31(个)8,即再减去31×8即可。

6. (1)推理意识 笑笑把笔记本密码锁的密码☆△☆给忘记了,根据下面的线索可知密码是(393)。
线索①：480÷[(☆+37)×2]= 6
线索②：[(280+260)÷△]×20= 1200
(2)运算能力 定义两种新运算：aΩb= a-b+1,aωb= a×b+1,将 Ω、ω 和括号填入下面的式子,使得等号成立(不能用别的计算符号)：
7 3 4 5 = 2
(7ω3)Ω(4ω5)

答案：
(1)393
提示:480÷[(☆+37)×2]=6,则(☆+37)×2=480÷6=80,☆+37=80÷2=40,☆=40 - 37=3;[(280+260)÷△]×20=1200,则(280+260)÷△=1200÷20=60,△=(280+260)÷60=540÷60=9。
(2)(7ω3)Ω(4ω5)=2
提示:观察题目,“ω”会导致结果变大,“Ω”会让前后两个数大致“抵消”掉。因为给出的数较大,而结果较小,所以应该把两种运算结合使用。

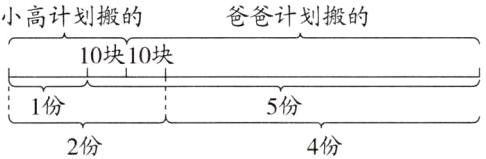
8. 应用意识 爸爸和小高一起搬砖头,原计划爸爸搬其中的一些,小高搬剩余的砖头。父子二人发现,如果爸爸帮小高搬 10 块,那么爸爸所搬的砖头数是小高的 5 倍；如果小高帮爸爸搬 10 块,那么爸爸所搬的砖头数是小高的 2 倍,原计划爸爸搬多少块砖头,小高搬多少块砖头?

答案：
10+10=20(块) 小高:20×1+10=30(块) 爸爸:20×5 - 10=90(块)
提示:由题意可知砖头的总数是不变量,作图如下,可以看出如果把爸爸帮小高搬10块后小高搬的砖头数看作1份,那么砖头总数一共有6份,如果小高帮爸爸搬10块,那么小高搬的砖头数就是2份,因此其中的1份是20块。