《2025年学霸甘肃少年儿童出版社四年级数学上册苏教版》

1. 四(2)班的同学正在进行游艺活动,抽签决定接下来表演的节目,一共做了这些签：

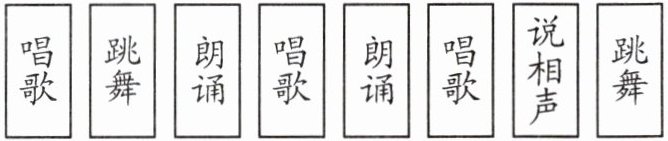
(1) 宋颜准备抽一张签,抽到的签有(4)种可能。
(2) 宋颜抽到(唱歌)签的可能性最大,抽到(跳舞)签与(朗诵)签的可能性相等,抽到(说相声)签的可能性最小。

答案： 1.
(1)4
(2)唱歌 跳舞 (朗诵) (说相声)

2. 判断题。
(1) 有4个红球和4个白球,每次任意摸一个球后放回再摸,一共摸了60次,摸出红球一定是30次。(×)
(2) 东东从一个袋子里摸了6次,摸到的全是白球,袋子里装的一定都是白球。(×)
(3) 下面每个盒子中都只有3枚白棋子,在③号盒子中摸到白棋子的可能性最大。(×)

答案：
(1) ×
解析：虽然红球和白球的数量相同，每次摸球的结果都是独立的，且摸出红球和白球的概率相等，均为$\frac{4}{4 + 4}=\frac{1}{2}$，但摸60次并不意味着红球一定会恰好出现30次，实际摸球结果会有波动。
答案：摸出红球不一定是30次。
(2) ×
解析：仅根据6次摸球结果都是白球，不能确定袋子里装的一定都是白球，因为摸球次数较少，存在偶然性，袋子里可能还有其他颜色的球。
答案：袋子里装的不一定都是白球。
(3) ×
解析：已知每个盒子中都只有3枚白棋子，那么每个盒子摸到白棋子的可能性都是$100\%$，所以三个盒子摸到白棋子的可能性一样大。
答案：在③号盒子中摸到白棋子的可能性不是最大的，三个盒子摸到白棋子可能性一样大。

3. 在下面的卡片上写出符合要求的汉字。
(1) 不可能抽到偏旁是“氵”的汉字。
你 我 他 们 你 我 他
(2) 可能抽到“亻”“讠”“刂”三种偏旁的汉字,且抽到偏旁是“讠”的可能性最大。
说 话 讲 你 们 到 利

答案：
(1) 你 我 他 们 你 我 他
(2) 说 话 讲 你 们 到 利

4. 下面是明明玩摸方块游戏的结果,他最可能摸的是第(②)个盒子里的方块。

答案： 解析：本题考查可能性的大小。
第一个盒子中白色方块有$6$个，黑色方块有$2$个，白色方块数量多，摸出白色方块的可能性大；
第二个盒子中白色方块有$3$个，黑色方块有$4$个，黑色方块数量多，摸出黑色方块的可能性大；
第三个盒子中白色方块有$6$个，黑色方块有$1$个，白色方块数量多，摸出白色方块的可能性大。
明明摸出白色方块次数多，摸出黑色方块次数少，所以他最可能摸的是第二个盒子里的方块。
答案：②。

5. 如图,口袋里放了8个球。

(1) 要使摸到白球、黑球的可能性相等,可以再放入(2)个(黑)球或拿出(2)个(白)球。
(2) 如果放入n个红球后,那么每次摸到红球的可能性大一些,n最小是(6)。

答案： 解析：本题主要考查了可能性大小与球的数量关系。
(1)已知口袋里一共有8个球，要使摸到白球、黑球的可能性相等，根据可能性大小与球的数量有关，数量相等时，摸到的可能性相等。
现在白球和黑球数量不相等，一种方法是增加白球数量，使其和黑球数量相等，现在黑球有3个，白球有$8 - 3 = 5$个，所以应再放入$5 - 3 = 2$个黑球；
另一种方法是减少白球数量，使其和黑球数量相等，即拿出$5 - 3 = 2$个白球。
故本题答案为：2；黑；2；白。
(2)已知放入n个红球后，每次摸到红球的可能性大一些。
现在口袋里白球有5个，黑球有3个，要使摸到红球可能性大，那么红球的数量要比白球数量多，白球有5个，所以红球至少要有$5 + 1 = 6$个，原来没有红球，所以n最小是6。
故本题答案为：6。