《2025年学霸甘肃少年儿童出版社四年级数学上册苏教版》

1.

(②)与(④)从右面看到的图形相同；从③的右面与从(④)的(上)面看到的图形相同；从①的上面与从(③)的(前)面看到的图形相同。

答案： ② ④ ④ 上 ③ 前

2. 用3个同样大的正方体横着摆成一排,摆成一个较大的长方体,画出从前面、右面、上面看到的图形。

答案：
前面: 右面: 上面:

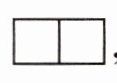
3. (1)用6个同样大的正方体摆一个长方体,从右面看是$□ □$,画出从前面和上面看的图形。


(2)用8个同样大的正方体摆一个长方体,使它从前面、右面、上面看到的图形都不相同。按要求画出看到的图形。

(3)用同样大的正方体搭一个立体图形,从前面、上面、右面看到的图形都是$\begin{array}{ll}□ & □ \\ □ & □\end{array}$\begin{array}{ll}□ & □ \\ □ & □ $,最多用( )个正方体。(4)用12个同样大的正方体摆一个长方体有( )种摆法。如果它从前面和上面看都是$\begin{array}{lll}□ & □ & □ \\ □ & □ & □\end{array}$\begin{array}{lll}□ & □ & □ \\ □ & □ & □ $,这时它从右面看是( )。

答案：
3.
(1)前面:□□□ 上面:
(2)答案不唯一,如:前面: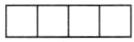 右面: 上面:□□□□
(3)8
提示:从三个面看到的图形都是相同的,所以搭成的这个立体图形可以是一个正方体,一共有两层,每层4个,最多用8个同样大的正方体。
(4)4
提示:12可以表示为3个数的乘积:12=1×1×12;12=1×2×6;12=1×3×4;12=2×2×3,所以用12个大小相同的正方体摆一个较大的长方体一共有4种摆法。如果它从前面和上面看都是,说明从右面看有2列2行,所以从右面看是

4. 如图的图形是由( )个同样大的小正方体拼成的,至少再添( )个就能拼成一个较大的长方体,这个长方体从前面、上面、右面看分别是什么图形？画一画。

答案：
4. 11 7 前面: 上面: 右面:
提示:图形从上往下一层层地数,分别有正方体1个、4个、6个,共有1+4+6=11(个),拼成大长方体,则每层有6个小正方体,有3层,一共需要6×3=18(个),还缺18-11=7(个)。