《2025年亮点给力提优课时作业本七年级数学上册苏科版》

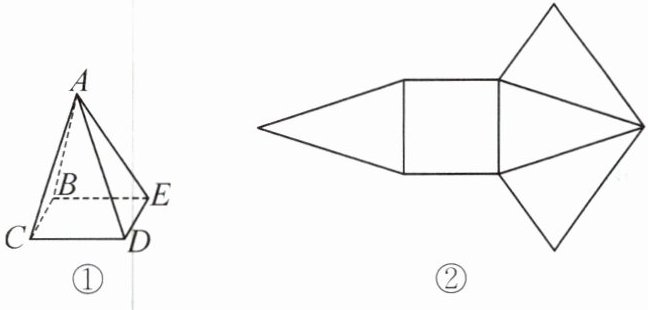
1. 将图①中的正四棱锥沿着其中的四条边剪开后,形成的表面展开图如图②所示.下列各组边中,可以为剪开的四条边的是(D)
A. $AC$,$AD$,$BC$,$DE$
B. $AB$,$BE$,$DE$,$CD$
C. $AC$,$BC$,$AE$,$DE$
D. $AC$,$AD$,$AE$,$BC$

答案： 解：正四棱锥底面为四边形CDEB（假设），侧面有四个三角形：ABC、ABD、ABE、ADE（根据顶点A及底面顶点C、D、E、B）。表面展开图需剪开4条棱，且展开后各面相连。
分析选项：
A选项：剪开AC、AD、BC、DE。底面四边形CDEB中，BC、DE被剪开，剩余CD、EB未剪，侧面ABC、ABD被剪AC、AD，仅剩AB相连，可能形成展开图，但需验证其他选项。
B选项：剪开AB、BE、DE、CD。AB为顶点到底面顶点的棱，剪开AB会使侧面与顶点分离，无法形成完整展开图，排除。
C选项：剪开AC、BC、AE、DE。底面四边形中BC、DE被剪，侧面ABC剪AC、BC后仅剩AB，侧面ABE剪AE后仅剩AB，底面CD、EB未剪，可能形成展开图，但展开图形状与图②对比，两侧三角形分布不符，排除。
D选项：剪开AC、AD、AE、BC。AC、AD、AE为顶点A到三个底面顶点的棱，仅剩AB未剪，BC为底面棱，底面剩余CD、DE、EB，展开后会有三个侧面三角形（ACD、ADE、ABE）围绕A，底面四边形CDEB与ABC相连，符合图②中间为四边形，两侧各两个三角形的展开形状。
综上，正确答案为D。
答案：D

2. 如图是一个对面图案均相同的正方体礼品盒,则这个正方体礼品盒的表面展开图可能是(B)

答案： 【解析】：
本题考查正方体展开图，考查空间想象能力。
我们需要根据正方体的特性，即相对的面在展开图中不会相邻，来判断哪个选项是正确的展开图。
我们可以先将选项A进行折叠，观察它的六个面，会发现“太阳”面相邻的是两个“笑脸”面，而在题目所给的立体图中，“太阳”面相邻的是一个“笑脸”面和一个“爱心”面，所以A选项错误。
同样，折叠选项C，会发现“爱心”面相邻的是两个“笑脸”面，这也与题目所给的立体图不符，所以C选项错误。
而折叠选项B，会发现它的六个面与题目所给的立体图完全一致，所以B选项是正确的。
【答案】：B

3. 如图是一个切去了一个角的正方体纸盒.现将纸盒剪开展成平面图形,则表面展开图不可能是(D)

答案： 解：D

4. 新素养 空间观念 如图是一个正方体纸盒的表面展开图,则这个正方体可能是(D)

答案： 【解析】：
首先，我们需要理解正方体的展开图如何折叠成正方体。这个展开图包含六个面，其中两个面带有圆点，两个面被涂成阴影，还有两个空白面。
接下来，我们逐一分析选项：
A选项：在A中，圆点面和阴影面在折叠后不应该相邻，但在A中它们是相邻的，所以A选项错误。
B选项：在B中，两个阴影面在折叠后应该是相对的，但在B中它们是相邻的，所以B选项错误。
C选项：在C中，两个圆点面在折叠后应该是相对的，但在C中，一个圆点面与一个阴影面相邻，这与展开图不符，所以C选项错误。
D选项：在D中，两个圆点面是相对的，两个阴影面也是相对的，且空白面与阴影面和圆点面的相邻关系也符合展开图，所以D选项正确。
【答案】：D。

5. 六个正方体$A$,$B$,$C$,$D$,$E$,$F$的可见部分如图①所示,图②是其中某些正方体的表面展开图,那么可能的正方体是______.(填字母)


C

答案： 【解析】：
本题考查正方体的展开图。
首先，需要注意每个正方体的可见部分，然后将其与展开图进行对比。
图②的展开图中有三个带斜线的面，且都相邻。
逐一分析每个正方体：
A正方体：有两个相邻的面带有斜线，但第三个面不带斜线，因此不符合。
B正方体：有两个相邻的面带有斜线，但第三个面不带斜线，因此不符合。
C正方体：有三个相邻的面都带有斜线，符合展开图的特征。
D正方体：只有一个面带有斜线，因此不符合。
E正方体：有两个相邻的面带有斜线，但第三个面不带斜线，且其斜线面的相对位置关系与展开图不符，因此不符合。
F正方体：虽然有三个带斜线的面，但它们不是都相邻，因此不符合。
【答案】：C

6. 如图,一只虫子从圆锥底面点$A处沿着侧面爬行一圈到点O$处,请画出它爬行的最短路线.(可添加辅助图说明)

答案： 解：1. 将圆锥侧面沿过点A的母线展开，得到一个扇形，点A在扇形弧的一个端点，点O为扇形的圆心。
2. 在展开的扇形中，连接点A与点O，所得线段AO即为虫子爬行的最短路线。
3. 将扇形还原为圆锥侧面，线段AO在圆锥侧面上的位置即为所求最短路线。