第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
10. (2025·江苏连云港期末)如图,将边长分别为1,2,3,5,…的若干正方形按一定的规律拼成不同的长方形,依次记作长方形①、长方形②、长方形③、长方形④、…按此规律,解答下列问题:
(1)长方形ⓝ中,正方形的个数是______
(2)求长方形⑥的周长.
解:长方形①中正方形边长为1,1,长=1+1=2,宽=1,周长=2×(2+1)=6;
长方形②中正方形边长为1,1,2,长=1+2=3,宽=1+1=2,周长=2×(3+2)=10;
长方形③中正方形边长为1,1,2,3,长=2+3=5,宽=1+3=4,周长=2×(5+4)=18;
长方形④中正方形边长为1,1,2,3,5,长=3+5=8,宽=2+5=7,周长=2×(8+7)=30;
规律:后一个长方形长=前一个长方形长+宽,宽=前一个长方形长;
长方形⑤长=8+7=15,宽=8,周长=2×(15+8)=46;
长方形⑥长=15+8=23,宽=15,周长=2×(23+15)=76。
答:长方形⑥的周长为76。
(1)长方形ⓝ中,正方形的个数是______
n+1
;(2)求长方形⑥的周长.
解:长方形①中正方形边长为1,1,长=1+1=2,宽=1,周长=2×(2+1)=6;
长方形②中正方形边长为1,1,2,长=1+2=3,宽=1+1=2,周长=2×(3+2)=10;
长方形③中正方形边长为1,1,2,3,长=2+3=5,宽=1+3=4,周长=2×(5+4)=18;
长方形④中正方形边长为1,1,2,3,5,长=3+5=8,宽=2+5=7,周长=2×(8+7)=30;
规律:后一个长方形长=前一个长方形长+宽,宽=前一个长方形长;
长方形⑤长=8+7=15,宽=8,周长=2×(15+8)=46;
长方形⑥长=15+8=23,宽=15,周长=2×(23+15)=76。
答:长方形⑥的周长为76。
答案:
(1)n+1
(2)解:长方形①中正方形边长为1,1,长=1+1=2,宽=1,周长=2×(2+1)=6;
长方形②中正方形边长为1,1,2,长=1+2=3,宽=1+1=2,周长=2×(3+2)=10;
长方形③中正方形边长为1,1,2,3,长=2+3=5,宽=1+3=4,周长=2×(5+4)=18;
长方形④中正方形边长为1,1,2,3,5,长=3+5=8,宽=2+5=7,周长=2×(8+7)=30;
规律:后一个长方形长=前一个长方形长+宽,宽=前一个长方形长;
长方形⑤长=8+7=15,宽=8,周长=2×(15+8)=46;
长方形⑥长=15+8=23,宽=15,周长=2×(23+15)=76。
答:长方形⑥的周长为76。
(1)n+1
(2)解:长方形①中正方形边长为1,1,长=1+1=2,宽=1,周长=2×(2+1)=6;
长方形②中正方形边长为1,1,2,长=1+2=3,宽=1+1=2,周长=2×(3+2)=10;
长方形③中正方形边长为1,1,2,3,长=2+3=5,宽=1+3=4,周长=2×(5+4)=18;
长方形④中正方形边长为1,1,2,3,5,长=3+5=8,宽=2+5=7,周长=2×(8+7)=30;
规律:后一个长方形长=前一个长方形长+宽,宽=前一个长方形长;
长方形⑤长=8+7=15,宽=8,周长=2×(15+8)=46;
长方形⑥长=15+8=23,宽=15,周长=2×(23+15)=76。
答:长方形⑥的周长为76。
11. 新趋势传统文化1905年清朝学堂的课本中用“$ \frac { \text { 五 } } { \text { 甲 } ^ { 2 } } \top \frac { \text { 三 } } { \text { 丙 } } \perp \frac { \text { 四 } } { \text { 甲 } \text { 乙 } ^ { 2 } } $”来表示代数式$ \frac { a ^ { 2 } } { 5 } - \frac { c } { 3 } + \frac { a b ^ { 2 } } { 4 } $,则“$ \frac { \text { 三 } } { \text { 甲 } \text { 乙 } ^ { 2 } } \perp \frac { \text { 二 } } { \text { 甲 } ^ { 2 } \text { 乙 } } $”表示的代数式为(
A.$ \frac { a b ^ { 2 } } { 3 } + \frac { a ^ { 2 } b } { 2 } $
B.$ \frac { a b ^ { 2 } } { 3 } - \frac { a ^ { 2 } b } { 2 } $
C.$ \frac { 3 } { a b ^ { 2 } } + \frac { 2 } { a ^ { 2 } b } $
D.$ \frac { 3 } { a b ^ { 2 } } - \frac { 2 } { a ^ { 2 } b } $
A
)A.$ \frac { a b ^ { 2 } } { 3 } + \frac { a ^ { 2 } b } { 2 } $
B.$ \frac { a b ^ { 2 } } { 3 } - \frac { a ^ { 2 } b } { 2 } $
C.$ \frac { 3 } { a b ^ { 2 } } + \frac { 2 } { a ^ { 2 } b } $
D.$ \frac { 3 } { a b ^ { 2 } } - \frac { 2 } { a ^ { 2 } b } $
答案:
解:由题意知,“五”对应5,“甲”对应a,“丙”对应c,“乙”对应b;“$\frac{\text{五}}{\text{甲}^2}$”表示$\frac{a^2}{5}$,即“$\frac{\text{数字}}{\text{文字组合}}$”表示“$\frac{\text{文字组合对应的代数式}}{\text{数字}}$”;“T”表示“$-$”,“⊥”表示“$+$”。
则“$\frac{\text{三}}{\text{甲乙}^2}$”表示$\frac{ab^2}{3}$,“$\frac{\text{二}}{\text{甲}^2\text{乙}}$”表示$\frac{a^2b}{2}$,“⊥”表示“$+$”。
所以“$\frac{\text{三}}{\text{甲乙}^2}\perp\frac{\text{二}}{\text{甲}^2\text{乙}}$”表示的代数式为$\frac{ab^2}{3}+\frac{a^2b}{2}$。
答案:A
则“$\frac{\text{三}}{\text{甲乙}^2}$”表示$\frac{ab^2}{3}$,“$\frac{\text{二}}{\text{甲}^2\text{乙}}$”表示$\frac{a^2b}{2}$,“⊥”表示“$+$”。
所以“$\frac{\text{三}}{\text{甲乙}^2}\perp\frac{\text{二}}{\text{甲}^2\text{乙}}$”表示的代数式为$\frac{ab^2}{3}+\frac{a^2b}{2}$。
答案:A
12. 观察下列数表:
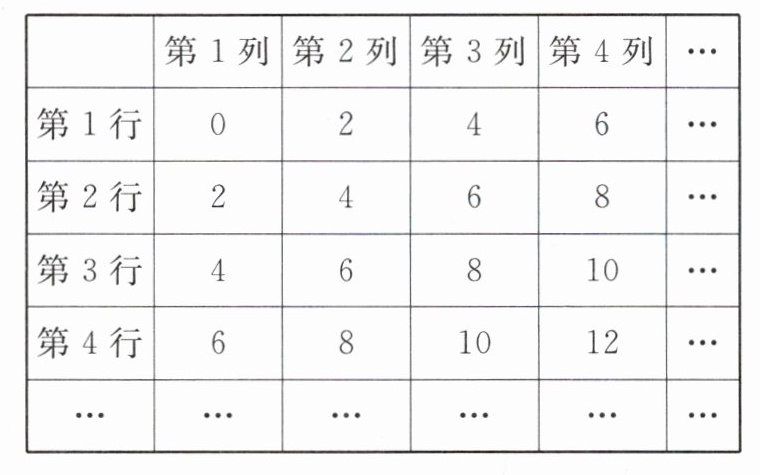
根据数表所反映的规律,猜想第6行第6列的数为

根据数表所反映的规律,猜想第6行第6列的数为
60
,第n行第n列的数为2n²-2n
.
答案:
1. 先分析第$n$行第$n$列数的规律:
第$1$行第$1$列的数是$0 = 2×(1 - 1)$;
第$2$行第$2$列的数是$4 = 2×(2 - 1)+2×(2 - 1)=2×(2 - 1)×2=2×(2 - 1)×2 = 2×(2×2 - 2)=2×(2^{2}-2)$;
第$3$行第$3$列的数是$8 = 2×(3 - 1)+2×(3 - 1)+2×(3 - 1)=2×(3 - 1)×3=2×(3^{2}-3)$;
第$4$行第$4$列的数是$14 = 2×(4 - 1)+2×(4 - 1)+2×(4 - 1)+2×(4 - 1)=2×(4 - 1)×4=2×(4^{2}-4)$;
一般地,对于第$n$行第$n$列的数$a_{n}$,根据上述规律可得$a_{n}=2(n^{2}-n)$。
2. 再求第$6$行第$6$列的数:
当$n = 6$时,把$n = 6$代入$a_{n}=2(n^{2}-n)$中。
则$a_{6}=2×(6^{2}-6)$。
先计算$6^{2}-6=36 - 6=30$,再计算$2×30 = 60$。
所以第$6$行第$6$列的数为$60$,第$n$行第$n$列的数为$2n^{2}-2n$。
故答案依次为:$60$;$2n^{2}-2n$。
第$1$行第$1$列的数是$0 = 2×(1 - 1)$;
第$2$行第$2$列的数是$4 = 2×(2 - 1)+2×(2 - 1)=2×(2 - 1)×2=2×(2 - 1)×2 = 2×(2×2 - 2)=2×(2^{2}-2)$;
第$3$行第$3$列的数是$8 = 2×(3 - 1)+2×(3 - 1)+2×(3 - 1)=2×(3 - 1)×3=2×(3^{2}-3)$;
第$4$行第$4$列的数是$14 = 2×(4 - 1)+2×(4 - 1)+2×(4 - 1)+2×(4 - 1)=2×(4 - 1)×4=2×(4^{2}-4)$;
一般地,对于第$n$行第$n$列的数$a_{n}$,根据上述规律可得$a_{n}=2(n^{2}-n)$。
2. 再求第$6$行第$6$列的数:
当$n = 6$时,把$n = 6$代入$a_{n}=2(n^{2}-n)$中。
则$a_{6}=2×(6^{2}-6)$。
先计算$6^{2}-6=36 - 6=30$,再计算$2×30 = 60$。
所以第$6$行第$6$列的数为$60$,第$n$行第$n$列的数为$2n^{2}-2n$。
故答案依次为:$60$;$2n^{2}-2n$。
13. 新趋势推导探究为了美化城市,某商场在门前的空地上用花盆按如图所示的方式搭正方形花坛.
(1)填写下表:
|层数|1|2|3|
|----|----|----|----|
|花盆数|
(2)按这个规律搭下去,搭第6层正方形,需要多少盆花?
(3)如果某一层上有36盆花,那么这是第几层?
(4)你找到这个规律了吗?请用含n(n表示正方形的层数)的代数式把这个规律表示出来.
(1)填写下表:
|层数|1|2|3|
|----|----|----|----|
|花盆数|
4
|8
|12
|(2)按这个规律搭下去,搭第6层正方形,需要多少盆花?
解:由规律可知第n层花盆数为4n,当n=6时,4×6=24(盆)
(3)如果某一层上有36盆花,那么这是第几层?
解:设这是第n层,4n=36,解得n=9
(4)你找到这个规律了吗?请用含n(n表示正方形的层数)的代数式把这个规律表示出来.
解:第n层需要花盆数的代数式为4n
答案:
(1)
|层数|1|2|3|
|----|----|----|----|
|花盆数|4|8|12|
(2)解:由规律可知第n层花盆数为4n,当n=6时,4×6=24(盆)
(3)解:设这是第n层,4n=36,解得n=9
(4)解:第n层需要花盆数的代数式为4n
|层数|1|2|3|
|----|----|----|----|
|花盆数|4|8|12|
(2)解:由规律可知第n层花盆数为4n,当n=6时,4×6=24(盆)
(3)解:设这是第n层,4n=36,解得n=9
(4)解:第n层需要花盆数的代数式为4n
查看更多完整答案,请扫码查看


