《2025年亮点给力提优课时作业本七年级数学上册苏科版》

13.(3分)将正整数按如图所示的规律排列下去.若用有序数对$(m,n)表示第m$排,从左到右第$n$个数,如$(3,2)$表示整数5,则$(16,4)$表示的数是124.

答案： 124

14.(3分)如果一个四位自然数$M= \overline {abcd}$的各数位上的数字互不相等,且满足$\overline {ab}+\overline {cd}= 130$,那么称这个四位数为“大吉数”.若一个“大吉数”$M$的前三个数字组成的三位数$\overline {abc}$与后三个数字组成的三位数$\overline {bcd}$的和能被11整除,则满足条件的$M$的最大值是____9832.

答案： 9832

15.(3分)如图,长方形$ABCD$由4块小长方形拼成,其中小长方形②③的形状、大小完全相同,且长与宽的差为2.5,则小长方形④与小长方形①周长的差是10.

答案： 10

16.(3分)计算:$(1-\frac {1}{2}+\frac {1}{3}-\frac {1}{4}+... +\frac {1}{2011}-\frac {1}{2012})÷(\frac {1}{1007}+\frac {1}{1008}+... +\frac {1}{2012})=$1.

答案： 1 解析：$\left[\left(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{2011}+\frac{1}{2012}\right)-2×\left(\frac{1}{2}+\frac{1}{4}+\cdots+\frac{1}{2012}\right)\right]÷\left(\frac{1}{1007}+\frac{1}{1008}+\cdots+\frac{1}{2012}\right)=\left[\left(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{2011}+\frac{1}{2012}\right)-\left(1+\frac{1}{2}+\cdots+\frac{1}{1006}\right)\right]÷\left(\frac{1}{1007}+\frac{1}{1008}+\cdots+\frac{1}{2012}\right)=\left(\frac{1}{1007}+\frac{1}{1008}+\cdots+\frac{1}{2012}\right)÷\left(\frac{1}{1007}+\frac{1}{1008}+\cdots+\frac{1}{2012}\right)=1$.

17.(2025·江苏泰州期末·3分)如图,过数轴上表示1的点作数轴的垂线$l_{1}$,过数轴上表示2的点作数轴的垂线$l_{2}$,过数轴上表示3的点作数轴的垂线$l_{3}$,….已知点$A_{0}$表示的数为-1,将点$A_{0}沿直线l_{1}翻折得到点A_{1}$,将点$A_{1}沿直线l_{2}翻折得到点A_{2}$,将点$A_{2}沿直线l_{3}翻折得到点A_{3}$,…,则点$A_{2025}$表示的数为____.


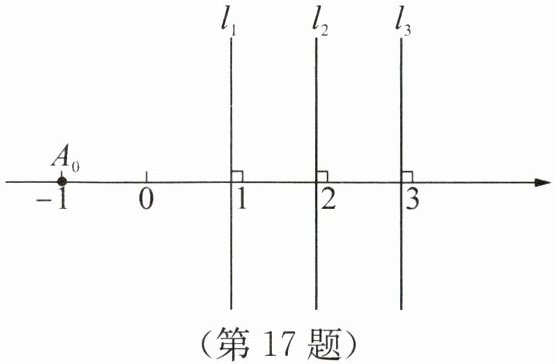
2027

答案： 2027 解析：由题意，得点$A_{0}$表示的数为-1，点$A_{1}$表示的数为$1×2-(-1)=3$，点$A_{2}$表示的数为$2×2-3=1$，点$A_{3}$表示的数为$2×3-1=5$，点$A_{4}$表示的数为$2×4-5=3$，点$A_{5}$表示的数为$2×5-3=7$，…，所以当n为奇数时，点$A_{n}$表示的数为$n+2$，所以点$A_{2025}$表示的数为$2025+2=2027$.

18.(3分)新素养抽象能力 对于三个数$a$,$b$,$c$,我们规定用$M\{ a,b,c\}$表示这三个数的平均数,用$min\{ a,b,c\}$表示这三个数中最小的数,例如:$M\{ -1,2,3\} = \frac {-1+2+3}{3}= \frac {4}{3},min\{ -1,2,3\} = -1$.若$M\{ 3,2x+1,4x-1\} = min\{ 2,-x+3,5x\}$,则$x$的值为$\frac{1}{2}$或$\frac{1}{3}$.

答案： $\frac{1}{2}$或$\frac{1}{3}$ 解析：由题意，得$M\{3,2x+1,4x-1\}=\frac{1}{3}[3+(2x+1)+(4x-1)]=2x+1$.因为$M\{3,2x+1,4x-1\}=\min\{2,-x+3,5x\}$，所以分类讨论如下：① 若$2x+1=2$，解得$x=\frac{1}{2}$，则$\min\{2,-x+3,5x\}=\min\left\{2,\frac{5}{2},\frac{5}{2}\right\}=2$，符合题意；② 若$2x+1=-x+3$，解得$x=\frac{2}{3}$，则$\min\{2,-x+3,5x\}=\min\left\{2,\frac{7}{3},\frac{10}{3}\right\}=2$，不合题意，舍去；③ 若$2x+1=5x$，解得$x=\frac{1}{3}$，则$\min\{2,-x+3,5x\}=\min\left\{2,\frac{8}{3},\frac{5}{3}\right\}=\frac{5}{3}$，符合题意.综上所述，x的值为$\frac{1}{2}$或$\frac{1}{3}$.

19.(3分)在数轴上有一点$A$,将点$A$向左移动2个单位长度得到点$B$,将点$B$向左移动4个单位长度得到点$C$,点$A$,$B$,$C分别表示有理数a$,$b$,$c$.若$a$,$b$,$c$这三个数的乘积为负数,且这三个数的和与其中的一个数相等,则$a$的值为4或3.

答案： 4或3 解析：由题意，得$b=a-2$，$c=b-4=a-6$，所以$a+b+c=3a-8$.因为a，b，c这三个数的和与其中的一个数相等，所以分类讨论如下：① 若$3a-8=a$，解得$a=4$，则$b=2$，$c=-2$，所以$abc=-16＜0$，符合题意；② 若$3a-8=a-2$，解得$a=3$，则$b=1$，$c=-3$，所以$abc=-9＜0$，符合题意；③ 若$3a-8=a-6$，解得$a=1$，则$b=-1$，$c=-5$，所以$abc=5＞0$，不合题意，舍去.综上所述，a的值为4或3.

20.(3分)在数轴上,点$A$,$C表示的数分别是a$,$c$,且$a$,$c满足等式(16+a)^{2}+|c-12|= 0$,点$B表示的数是多项式2x^{2}-4x+3$的一次项系数.点$A$,$B$,$C$在数轴上同时开始运动,点$A$向左运动,速度为每秒3个单位长度,点$B$,$C$均向右运动,速度分别为每秒3个单位长度和每秒4个单位长度,设运动的时间为$t\ s$,且点$A$,$B之间的距离表示为AB$,点$B$,$C之间的距离表示为BC$.若存在$m$,使得$AB-mBC的值不随t$的变化而变化,则$AB-mBC$的值是____-84.

答案： -84 解析：因为$(16+a)^{2}+|c-12|=0$，所以$16+a=0$，$c-12=0$，解得$a=-16$，$c=12$.因为点B表示的数是多项式$2x^{2}-4x+3$的一次项系数，所以点B表示的数是-4.由题意，得当运动的时间为t s时，点A，B，C表示的数分别是$-16-3t$，$-4+3t$，$12+4t$，所以$AB=-4+3t-(-16-3t)=6t+12$，$BC=12+4t-(-4+3t)=t+16$，所以$AB-mBC=6t+12-m(t+16)=(6-m)t+12-16m$.因为$AB-mBC$的值不随t的变化而变化，所以$6-m=0$，解得$m=6$，所以$AB-mBC=12-16×6=-84$.