《2025年通城学典全程测评卷九年级数学全一册苏科版》

21. (10分)小亮是个集邮爱好者,他收集了5张纪念邮票(除正面内容不同外,其余均相同),其中,1张是“冬奥会会徽”,2张是“吉祥物冰墩墩”,2张是“吉祥物雪容融”.现将5张邮票背面朝上,洗匀放好.
(1)小亮从中随机抽取一张邮票是“吉祥物雪容融”的概率是______$\frac{2}{5}$.
(2)小明发明了一种“邮票棋”比胜负的游戏,用小亮的三种邮票当作5颗棋子,其中“冬奥会会徽”邮票记作A棋,“吉祥物冰墩墩”邮票记作B棋,“吉祥物雪容融”邮票记作C棋.游戏规则:将这5颗棋子放入一个不透明的袋子中,摇匀后随机从5颗棋子中摸出1颗棋子,不放回,再摸出第2颗棋子.若摸到A棋,则小明胜;若摸到两颗相同的棋子,则小亮胜;其余情况视为平局,游戏重新进行.请你用列表或画树状图的方法验证这个游戏是否公平,并说明理由.
这个游戏不公平 理由:列表如下:
A　　　　B　　　　B　　　　C　　　　C
A　　　　　　　(B,A)　　(B,A)　　(C,A)　　(C,A)
B　　　(A,B)　　　　　　(B,B)　　(C,B)　　(C,B)
B　　　(A,B)　　(B,B)　　　　　　(C,B)　　(C,B)
C　　　(A,C)　　(B,C)　　(B,C)　　　　　　(C,C)
C　　　(A,C)　　(B,C)　　(B,C)　　(C,C)
由表,可知共有20种等可能的结果,其中摸到A棋的结果有8种,摸到两颗相同的棋子的结果有4种,
∴小明获胜的概率为$\frac{8}{20}$ = $\frac{2}{5}$,小亮获胜的概率为$\frac{4}{20}$ = $\frac{1}{5}$.
∵$\frac{1}{5}$ ≠ $\frac{2}{5}$,
∴这个游戏不公平.

答案：
(1)$\frac{2}{5}$ 解析:小亮从中随机抽取一张邮票是“吉祥物雪容融”的概率是$\frac{2}{5}$.
(2)这个游戏不公平 理由:列表如下:
A　　　　B　　　　B　　　　C　　　　C
A　　　　　　　(B,A)　　(B,A)　　(C,A)　　(C,A)
B　　　(A,B)　　　　　　(B,B)　　(C,B)　　(C,B)
B　　　(A,B)　　(B,B)　　　　　　(C,B)　　(C,B)
C　　　(A,C)　　(B,C)　　(B,C)　　　　　　(C,C)
C　　　(A,C)　　(B,C)　　(B,C)　　(C,C)
由表,可知共有20种等可能的结果,其中摸到A棋的结果有8种,摸到两颗相同的棋子的结果有4种,
∴小明获胜的概率为$\frac{8}{20}$ = $\frac{2}{5}$,小亮获胜的概率为$\frac{4}{20}$ = $\frac{1}{5}$.
∵$\frac{1}{5}$ ≠ $\frac{2}{5}$,
∴这个游戏不公平.

22. (14分)(2024·南京)某品牌汽车2月份至6月份销售量的月增量(单位:万辆)的折线统计图如图所示.

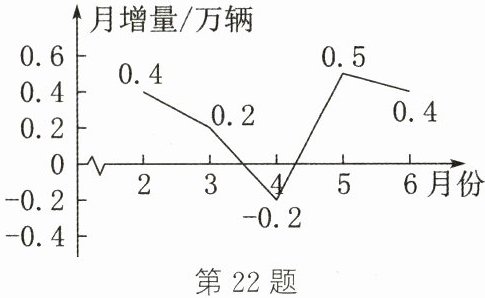
注:月增量= 当月的销售量-上月的销售量,月增长率= $\frac{月增量}{上月的销售量}$×100%.例如,8月份的销售量为2万辆,9月份的销售量为2.4万辆,那么9月份销售的月增量为2.4-2= 0.4(万辆),月增长率为20%.
(1)有下列说法:A. 2月份的销售量为0.4万辆;B. 2月份至6月份销售量的月增量的平均数为0.26万辆;C. 5月份的销售量最大;D. 5月份销售的月增长率最大.其中正确的是B(填字母).
(2)6月份的销售量比1月份增加了1.3万辆.
(3)2月份至4月份的月销售量持续减少,你同意这种观点吗?请说明理由.
不同意这种观点 理由:月增量为正,即当月销售量比上月增加;月增量为负,即当月销售量比上月减少.3月份的月增量为0.2万辆,0.2 ＞ 0,即3月份相比2月份的销售量是增加的,4月份的月增量为 - 0.2万辆,- 0.2 ＜ 0,即4月份相比3月份的销售量是减少的,即2月份至4月份的月销售量不是持续减少的.

答案：
(1)B 解析:A:
∵月增量 = 当月的销售量 - 上月的销售量,不知道1月份的销售量,
∴无法得到2月份的销售量.故选项错误,不符合题意;B:
∵(0.4 + 0.2 - 0.2 + 0.5 + 0.4)÷5 = 0.26(万辆),
∴2月份至6月份销售量的月增量的平均数为0.26万辆.故选项正确,符合题意;C:
∵6月份的月增量为0.4万辆,0.4 ＞ 0,
∴5月份的销售量小于6月份的销售量,即5月份的销售量不是最大的.故选项错误,不符合题意;D:
∵不知道1月份的销售量,
∴无法求得各月的销售量,无法计算月增长率.
∴不能判断5月份销售的月增长率最大.故选项错误,不符合题意.
(2)1.3 解析:设1月份的销售量为x万辆.
∴x + 0.4 + 0.2 - 0.2 + 0.5 + 0.4 = x + 1.3.
∴x + 1.3 - x = 1.3.
∴6月份的销售量比1月份增加了1.3万辆.
(3)不同意这种观点 理由:月增量为正,即当月销售量比上月增加;月增量为负,即当月销售量比上月减少.3月份的月增量为0.2万辆,0.2 ＞ 0,即3月份相比2月份的销售量是增加的,4月份的月增量为 - 0.2万辆,- 0.2 ＜ 0,即4月份相比3月份的销售量是减少的,即2月份至4月份的月销售量不是持续减少的.