《2025年通城学典全程测评卷九年级数学全一册苏科版》

11. 如图,这是一块直角三角形的空地,计划将涂色部分修建为花圃,已知AC的长为8米,AB的长为17米,涂色部分是△ABC的内切圆.一只小鸟随机落在这块空地上,则小鸟落在涂色部分上的概率是______.

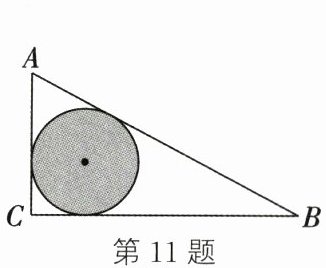
$\frac{3}{20}π$

答案： $\frac{3}{20}π$ 解析:
∵△ABC为直角三角形,AC的长为8米,AB的长为17米,
∴BC = 15米.
∴△ABC的内切圆半径 = $\frac{8 + 15 - 17}{2}$ = 3(米).
∴$S_{△ABC}$ = $\frac{1}{2}$AC·BC = $\frac{1}{2}$×8×15 = 60(平方米),$S_{圆}$ = π$r^{2}$ = π·$3^{2}$ = 9π(平方米).
∴小鸟落在涂色部分上的概率 = $\frac{9π}{60}$ = $\frac{3}{20}π$.

12. (2024·资阳)一个不透明的袋中装有6个白球和m个红球,这些球除颜色外无其他差别.充分搅匀后,从袋中随机取出一个球是白球的概率为$\frac{2}{5}$,则m=9.

答案： 9 解析:根据题意得,$\frac{6}{6 + m}$ = $\frac{2}{5}$,解得m = 9.经检验,m = 9是原方程的解.

13. 某商场举行活动,发放5000张奖券,在这些奖券中,设置如下奖项:
|奖项|现金100元|现金50元|现金20元|肥皂一盒|毛巾一条|
|数量/张|10|90|900|2000|2000|
如果张阿姨获得了一张奖券,那么她获得现金的概率是______$\frac{1}{5}$.

答案： $\frac{1}{5}$ 解析:5000张奖券中,可以获得现金的有10 + 90 + 900 = 1000(张),
∴张阿姨获得现金的概率是$\frac{1000}{5000}$ = $\frac{1}{5}$.

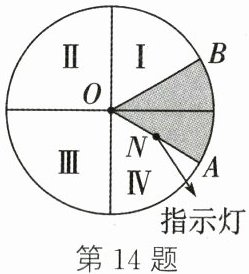
14. 如图,将一个圆盘四等分,并把四个区域分别标上Ⅰ、Ⅱ、Ⅲ、Ⅳ,只有区域Ⅰ为感应区域,圆心角为60°的扇形AOB绕点O转动.在半径OA上装有带指示灯的感应装置,当扇形AOB与区域Ⅰ有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为______$\frac{5}{12}$.

答案： $\frac{5}{12}$ 解析:如图,当扇形AOB落在区域Ⅰ时,指示灯会发光.假设扇形区域逆时针转动,当OB越过OE时,指示灯开始发光,当OB越过OC时,指示灯停止发光,此过程中OB转过的角度为60° + 90° = 150°.
∴指示灯发光的概率为$\frac{150°}{360°}$ = $\frac{5}{12}$.假设扇形区域顺时针旋转,当OA越过OF时,指示灯开始发光,当OA越过OD时,指示灯停止发光,此过程中OA转过的角度为60° + 90° = 150°.
∴指示灯发光的概率为$\frac{150°}{360°}$ = $\frac{5}{12}$.
∴指示灯发光的概率为$\frac{150°}{360°}$ = $\frac{5}{12}$.

15. (2024·呼和浩特)有4张分别印有卡通西游图案的卡片:唐僧、孙悟空、猪八戒、沙悟净.现将这4张卡片(除人物图案不同外,其余均相同)放在不透明的盒子中,搅匀后从中随机取出1张卡片,然后放回并搅匀,再从中随机取出1张卡片,则两次取到相同人物图案的卡片的概率为$\frac{1}{4}$.

答案： $\frac{1}{4}$ 解析:将“唐僧”图案记为“A”,将“孙悟空”图案记为“B”,将“猪八戒”图案记为“C”,将“沙悟净”图案记为“D”,画树状图如下图所示.共有16种等可能的结果,两次取到相同人物图案的卡片结果有(A,A)、(B,B)、(C,C)、(D,D),共4种,
∴两次取到相同人物图案的卡片概率 = $\frac{4}{16}$ = $\frac{1}{4}$.

16. (2024·北京)某厂加工了200个工件,质检员从中随机抽取10个工件检测了它们的质量(单位:g),得到的信息如下:50.03、49.98、50.00、49.99、50.02、49.99、50.01、49.97、50.00、50.02.当一个工件的质量x(单位:g)满足49.98≤x≤50.02时,评定该工件为一等品.根据以上信息,估计这200个工件中一等品的个数是______160.

答案： 160 解析:
∵满足49.98≤x≤50.02时,评定该工件为一等品,
∴抽取的10个工件中,一等品的有49.98 g、50.00 g、49.99 g、50.02 g、49.99 g、50.01 g、50.00 g、50.02 g,共计8个.
∴估计这200个工件中一等品的个数是200×$\frac{8}{10}$ = 160.

17. (8分)新考法探究题刘强同学为了调查全市(包括城区和农村)初中生人数,他对自己所在城区人口和城区初中生人数进行了调查:城区人口约为3万人,城区初中生人数约为1200.全市人口实际约为300万人,为此他推断全市初中生人数为12万.但市教育局提供的全市初中生人数约8万,与估计数据有很大偏差.请你帮助刘强同学分析一下数据偏差过大的原因是什么.如果你是刘强,应该怎样进行调查?

答案： 由于全市初中生既有农村的、又有城区的,故在选取样本时要既有农村人口,又有城区人口.刘强同学只对自己所在城区人口和城区初中生人数进行了调查,故此样本不具有代表性.可以在城区中随机选择两个社区,在农村中随机选择两个乡镇进行调查(合理即可)