《2025年通城学典全程测评卷九年级数学全一册苏科版》

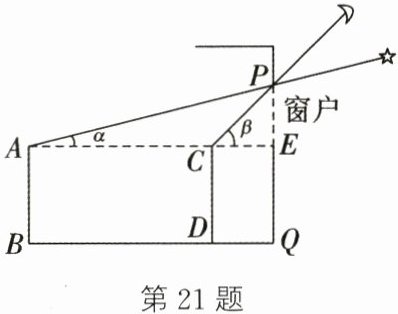
21. (10分)(2024·河北)我国的探月工程激发了同学们对太空的兴趣.某晚,淇淇在家透过窗户的最高点P恰好看到一颗星星,此时淇淇距窗户的水平距离BQ= 4m,仰角为α;淇淇向前走了3m后到达点D,透过点P恰好看到月亮,仰角为β,如图所示.已知淇淇的眼睛与水平地面BQ的距离AB= CD= 1.6m,点P到BQ的距离PQ= 2.6m,AC的延长线交PQ于点E(图中所有点均在同一平面内).求:
(1) β的大小及$\tan\alpha$的值;
(2) CP的长及$\sin∠APC$的值.

答案：

(1) 由题意,可得PQ⊥AE,PQ=2.6 m,AB=CD=EQ=1.6 m,AE=BQ=4 m,AC=BD=3 m.
∴CE=4-3=1(m),PE=2.6-1.6=1(m),∠CEP=90°.
∴CE=PE.
∴β=∠CPE=45°,tanα=tan∠PAE=$\frac{PE}{AE}$=$\frac{1}{4}$。
(2)
∵CE=PE=1 m,∠CEP=90°,
∴CP=$\sqrt{1² + 1²}$=$\sqrt{2}$(m).如图,过点C作CH⊥AP于点H.
∵tanα=tan∠PAE=$\frac{CH}{AH}$=$\frac{1}{4}$,
∴设CH=x m,则AH=4x m.
∴x²+(4x)²=9.
∴x=$\frac{3\sqrt{17}}{17}$.
∴CH=$\frac{3\sqrt{17}}{17}$ m.
∴sin∠APC=$\frac{CH}{CP}$=$\frac{\frac{3\sqrt{17}}{17}}{\sqrt{2}}$=$\frac{3\sqrt{34}}{34}$。
　　　　　　

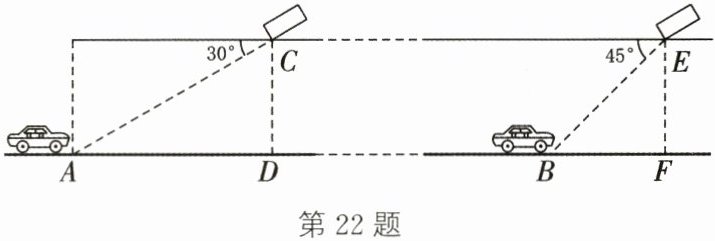
22. (10分)(2023·凉山)高速公路管理部门在某隧道内的点C、E两处安装了测速仪,该段隧道的截面示意图如图所示,图中所有点都在同一平面内,且A、D、B、F四点在同一直线上.点C、点E到AB的距离分别为CD、EF,且CD= EF= 7m,CE= 895m,在点C处测得小型汽车在点A的俯角为30°,在点E处测得小型汽车在点B的俯角为45°,小型汽车在隧道内从点A行驶到点B所用时间为45s(参考数据:$\sqrt{2}≈1.4$,$\sqrt{3}≈1.7$).
(1) 求A、B两点之间的距离(结果精确到1m).
(2) 若该隧道限速80km/h,判断小型汽车从点A行驶到点B是否超速.并通过计算说明理由.

答案：
(1) 根据题意,得四边形CDFE是矩形,∠CAD=30°,∠EBF=45°,
∴DF=CE=895 m.在Rt△EBF中,tan45°=$\frac{EF}{BF}$=1,BF=EF=7 m.
∴DB=DF-BF=895-7=888(m).在Rt△ACD中,tan30°=$\frac{CD}{AD}$=$\frac{\sqrt{3}}{3}$,AD=$\frac{CD}{\frac{\sqrt{3}}{3}}$=7$\sqrt{3}$≈11.9(m).
∴AB=AD+BD=11.9+888=899.9(m)≈900(m).
∴A、B两点之间的距离约为900 m。
(2)
∵小型汽车从点A行驶到点B所用时间为45 s,速度为900÷45=20(m/s).
∵20 m/s=20×3.6=72 km/h,72＜80,
∴小型汽车从点A行驶到点B没有超速。