《2025年通城学典全程测评卷九年级数学全一册苏科版》

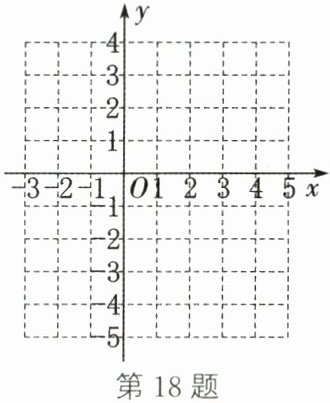
18. (8分)(2024·苏州姑苏段考)已知二次函数$y= ax^{2}+bx+c(a≠0)$的图像上部分点的横坐标、纵坐标的对应值如表:
|x|…|0|1|2|3|4|…|
|y|…|-3|-4|-3|0|5|…|
(1)在如图所示的平面直角坐标系中画出函数图像,并求出图像与x轴的交点坐标;
(2)当x______时,y随x的增大而减小;
(3)当$-1≤x≤4$时,y的取值范围是______.

答案：
（1）根据表格中所给的数据在平面直角坐标系中描点、连线,画出的图像如图所示.
∵二次函数$y = ax^{2}+bx + c(a\neq0)$的图像经过点$(0,-3)$,
∴$y = ax^{2}+bx - 3$.把$(1,-4)$、$(3,0)$分别代入函数表达式得,$\begin{cases}-4=a + b-3,\\0=9a + 3b-3,\end{cases}$解得$\begin{cases}a = 1,\\b = - 2.\end{cases}$
∴二次函数的表达式为$y = x^{2}-2x - 3$.令$y = 0$,则$x^{2}-2x - 3 = 0$,解得$x_{1}=-1$,$x_{2}=3$.
∴图像与x轴的交点坐标为$(-1,0)$和$(3,0)$；（2）$＜1$ 解析:由图像,知当$x＜1$时,$y$随$x$的增大而减小；（3）$-4\leq y\leq5$ 解析:由图像和表,知当$-1\leq x\leq4$时,$y$的取值范围是$-4\leq y\leq5$.
　　　　　　

19. (8分)新趋势跨学科我国古诗词源远流长.某校以“赏诗词之美、寻文化之根、铸民族之魂”为主题,组织学生开展古诗词知识竞赛活动.为了解学生对古诗词的掌握情况,该校随机抽取了部分学生的竞赛成绩,将成绩分为A、B、C、D四个等级,并绘制成如图所示的两幅不完整的统计图.
(1)本次共抽取了______名学生的竞赛成绩,并补全条形统计图;
(2)学校在竞赛成绩为A等级中的甲、乙、丙、丁这4名学生里,随机选取2人参加经典诵读活动,用画树状图或列表法求出甲、乙两人中恰好有1人被选中的概率.

答案：
（1）400 补全条形统计图如图①所示 解析:$80÷20\% = 400$(名),
∴D等级的人数为$400 - 120 - 160 - 80 = 40$；（2）画树状图如图②所示,共有12种等可能的结果,其中甲、乙两人中恰好有1人被选中的结果有8种.
∴甲、乙两人中恰好有1人被选中的概率为$\frac{8}{12}=\frac{2}{3}$