《2025年通城学典全程测评卷九年级数学全一册苏科版》

9. (2024·扬州邗江模拟)已知线段$a= \sqrt {7}-1,b= \sqrt {7}+1$,则a、b的比例中项为$\sqrt{6}$.

答案： $\sqrt{6}$ 解析:设a、b的比例中项为x.
∵$a=\sqrt{7}-1$,$b=\sqrt{7}+1$,
∴$x^{2}=ab=(\sqrt{7}-1)(\sqrt{7}+1)=6$.
∴$x=\sqrt{6}$(舍去负值),即a、b的比例中项为$\sqrt{6}$.

10. 已知$k＞0$,且关于x的方程$3kx^{2}+12x+k+1= 0$有两个相等的实数根,则k的值等于3.

答案： 3 解析:
∵关于x的方程$3kx^{2}+12x + k + 1 = 0$有两个相等的实数根,
∴$b^{2}-4ac = 144 - 4×3k×(k + 1)=0$,解得$k = - 4$或$k = 3$.
∵$k ＞ 0$,
∴$k = 3$.

11. (2024·扬州江都段考)已知$\odot O$的半径为5,弦$AB= 8$,则$\odot O$上到弦AB所在直线的距离等于1的点有______个.

答案：
4 解析:如图,过点O作半径$OD\perp AB$于点C,连接OA.
∵在$\odot O$中,弦$AB = 8$,
∴$AC=\frac{1}{2}AB = 4$.
∵$OA = 5$,
∴$OC=\sqrt{OA^{2}-AC^{2}} = 3$.
∴$CD = 5 - 3 = 2$.
∴在劣弧上点D到弦AB所在直线的距离为2.
∴在劣弧上有2个点到弦AB的距离为1,在优弧上有2个点到弦AB所在直线的距离为1.
∴$\odot O$上到弦AB所在直线的距离为1的点有4个.
　　　　　　　　

12. (2024·兴化段考)已知二次函数$y= -2(x-1)^{2}+k的图像上有A(-7,y_{1})$、$B(2,y_{2})$、$C(3,y_{3})$三个点,用“＜”连接$y_{1}$、$y_{2}$、$y_{3}$的结果是______$y_{1}＜y_{3}＜y_{2}$.

答案： $y_{1}＜y_{3}＜y_{2}$ 解析:
∵二次函数的表达式为$y = - 2(x - 1)^{2}+k$,$-2 ＜ 0$,
∴该函数图像开口向下,对称轴是直线$x = 1$.
∴图像上的点离对称轴越近,相对应的纵坐标越大.
∵二次函数$y = - 2(x - 1)^{2}+k$的图像上有$A(-7,y_{1})$、$B(2,y_{2})$、$C(3,y_{3})$三个点,
∴点A离对称轴最远,点B离对称轴最近.
∴$y_{1}＜y_{3}＜y_{2}$.

13. (2024·无锡惠山段考)一些木工师傅利用平行四边形的不稳定性制作了一种放缩尺,可将图形进行缩放.如图,四边形ABCD为平行四边形,$OD= AD= 1,AB= A'B= 2$,以点O为轴心,在点A处和点$A'$处安装制图笔,当点A处制图笔所画图形的面积为3时,点$A'$处制图笔所画图形的面积是______.

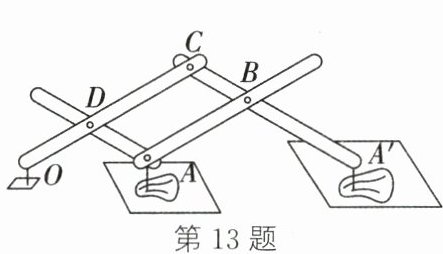
答案：
27 解析:如图,连接$OA'$.
∵四边形ABCD为平行四边形,
∴$BC = AD = 1$,$BC// AD$.
∴易得$A'C = 2 + 1 = 3$.由题意知点A在$OA'$上.
∵$BC// AD$,
∴$\triangle ADO\backsim\triangle A'CO$.
∵$\frac{A'C}{AD}=3$,
∴点$A'$处制图笔所画图形的面积与点A处制图笔所画图形的面积的比值为9.
∵点A处制图笔所画图形的面积为3,
∴点$A'$处制图笔所画图形的面积是27.
　　　　　　　

14. 如图,$\odot O$的半径为6,点P在$\odot O$上,点A在$\odot O$内,且$AP= 3$,过点A作AP的垂线交$\odot O$于点B、C.设$PB= x,PC= y$,则y与x之间的函数表达式为______.

答案：
$y=\frac{36}{x}(x＞0)$ 解析:如图,连接PO并延长交$\odot O$于点H,连接BH.由圆周角定理得,$\angle C=\angle H$,$\angle PBH = 90^{\circ}$.
∵$PA\perp BC$,
∴$\angle PAC = 90^{\circ}$.
∴$\angle PAC=\angle PBH$.
∴$\triangle PAC\backsim\triangle PBH$.
∴$\frac{PB}{PA}=\frac{PH}{PC}$,即$\frac{x}{3}=\frac{12}{y}$.
∴$y=\frac{36}{x}(x＞0)$.
　　　　　　　　

15. (2024·海安段考)下表记录了二次函数$y= ax^{2}+bx+2(a≠0)$中两个变量x与y的5组对应值,其中$x_{1}＜x_{2}＜1$.根据表中信息,当$-\frac {5}{2}＜x＜0$时,直线$y= k$与该二次函数图像有两个公共点,则k的取值范围是______.
|x|…|-5|$x_{1}$|$x_{2}$|1|3|…|
|y|…|m|0|2|0|m|…|

$2＜k＜\frac{8}{3}$

答案： $2＜k＜\frac{8}{3}$ 解析:由点的坐标,可得抛物线的对称轴为直线$x = - 1$.又由点$(x_{1},0)$、$(1,0)$以及抛物线的对称轴直线$x = - 1$,可得$x_{1}=-3$.设抛物线对应的函数表达式的顶点式为$y = a(x + 3)(x - 1)$.
∵$y = a(x + 3)(x - 1)=a(x^{2}+2x - 3)=ax^{2}+2ax - 3a$,即$y = ax^{2}+bx + 2(a\neq0)$,
∴$-3a = 2$,解得$a = -\frac{2}{3}$.
∴$y = -\frac{2}{3}x^{2}-\frac{4}{3}x + 2$.
∴当$x = -\frac{5}{2}$时,$y = -\frac{2}{3}×\frac{25}{4}-\frac{4}{3}×(-\frac{5}{2})+2=\frac{7}{6}$;当$x = 0$时,$y = 2$;当$x = - 1$时,$y = -\frac{2}{3}+\frac{4}{3}+2=\frac{8}{3}$.
∵当$-\frac{5}{2}＜x＜0$时,直线$y = k$与该二次函数图像有两个公共点.
∴$2＜k＜\frac{8}{3}$.

16. (2024·扬州江都段考)已知E是矩形ABCD的边BC上一点,$\frac {BE}{CE}= \frac {2}{3}$,连接AE,将$\triangle ABE$沿AE翻折.若点B的对应点$B'$正好落在矩形的对角线上,则$\frac {AB}{BC}$的值为______.

答案：
$\frac{2\sqrt{5}}{5}$或$\frac{\sqrt{10}}{5}$ 解析:设$BE = 2a$,$CE = 3a$,分两种情况:①点$B'$在AC上,如图①所示.由翻折可知,$B'E = BE = 2a$,$\angle AB'E=\angle B = 90^{\circ}$.
∴$\angle CB'E=\angle B = 90^{\circ}$.
∴$B'C=\sqrt{CE^{2}-B'E^{2}}=\sqrt{5}a$.
∴$\frac{B'E}{B'C}=\frac{2a}{\sqrt{5}a}=\frac{2\sqrt{5}}{5}$.
∵$\angle B=\angle CB'E = 90^{\circ}$,$\angle ACB=\angle ECB'$,
∴$\triangle ABC\backsim\triangle EB'C$.
∴$\frac{AB}{BC}=\frac{B'E}{B'C}=\frac{2\sqrt{5}}{5}$;②点$B'$在BD上,如图②所示.由翻折可知,$B'E = BE = 2a$,$AB = AB'$.
∴AE垂直平分$BB'$.
∴$\angle BAE+\angle ABD = 90^{\circ}$.
∵$\angle ABD+\angle CBD = 90^{\circ}$,
∴$\angle BAE=\angle CBD$.
∴$\triangle ABE\backsim\triangle BCD$.
∴$\frac{AB}{BE}=\frac{BC}{CD}$,即$\frac{AB}{2a}=\frac{5a}{AB}$.
∴$AB=\sqrt{10}a$.
∴$\frac{AB}{BC}=\frac{\sqrt{10}a}{5a}=\frac{\sqrt{10}}{5}$.综上所述,$\frac{AB}{BC}$的值为$\frac{2\sqrt{5}}{5}$或$\frac{\sqrt{10}}{5}$.
　　　

17. (8分)解方程:
(1)$3x(2x+1)= 2x+1$;
(2)$2x^{2}-5x+1= 0$.

答案： （1）$3x(2x + 1)=2x + 1$,$3x(2x + 1)-(2x + 1)=0$,$(2x + 1)(3x - 1)=0$.
∴$2x + 1 = 0$或$3x - 1 = 0$,解得$x_{1}=-\frac{1}{2}$,$x_{2}=\frac{1}{3}$；（2）
∵在$2x^{2}-5x + 1 = 0$中,$a = 2$,$b = - 5$,$c = 1$,
∴$b^{2}-4ac = (-5)^{2}-4×2×1 = 17＞0$.
∴方程有两个不相等的实数根.
∴$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}=\frac{5\pm\sqrt{17}}{4}$.
∴$x_{1}=\frac{5+\sqrt{17}}{4}$,$x_{2}=\frac{5-\sqrt{17}}{4}$