《2025年通城学典全程测评卷九年级数学全一册苏科版》

8. (2023·南京)如图,不等臂跷跷板AB的一端A碰到地面时,另一端B到地面的高度为60cm;当AB的一端B碰到地面时,另一端A到地面的高度为90cm,则跷跷板AB的支撑点O到地面的高度OH是 ( )


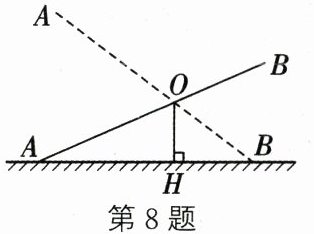
A.36cm
B.40cm
C.42cm
D.45cm

答案：
A 解析:如图①,过点B作BC⊥AH,垂足为C.
∵OH⊥AC,BC⊥AC,
∴∠AHO = ∠ACB = 90°.
∵∠BAC = ∠OAH,
∴△AOH∽△ABC.
∴$\frac{OH}{BC}=\frac{AO}{AB}$.
∴$\frac{OH}{60}=\frac{AO}{AB}$.如图②,过点A作AD⊥BH,垂足为D.
∵OH⊥BD,AD⊥BD,
∴∠OHB = ∠ADB = 90°.
∵∠ABD = ∠OBH,
∴△ABD∽△OBH.
∴$\frac{OH}{AD}=\frac{OB}{AB}$.
∴$\frac{OH}{90}=\frac{OB}{AB}$.
∴$\frac{OH}{60}+\frac{OH}{90}=\frac{AO}{AB}+\frac{OB}{AB}$.
∴$\frac{OH}{60}+\frac{OH}{90}=\frac{AB}{AB}$.
∴$\frac{OH}{60}+\frac{OH}{90}=1$,解得OH = 36cm.
∴跷跷板AB的支撑点O到地面的高度OH是36cm.

9. 甲地与乙地之间的实际距离约200千米,在比例尺为1:5000000的地图上,甲地与乙地之间的图上距离约4厘米.

答案： 4 解析:设甲地与乙地之间的图上距离为x厘米.200千米 = 20000000厘米,x:20000000 = 1:5000000,解得x = 4.

10. (2024·滨州)如图,在$\triangle ABC$中,点D、E分别在边AB、AC上.添加一个条件使$\triangle ADE \backsim \triangle ACB$,则这个条件可以是∠ADE = ∠C(写出一种情况即可).

答案： ∠ADE = ∠C(答案不唯一) 解析:
∵∠DAE = ∠CAB,
∴添加条件∠ADE = ∠C可判定△ADE∽△ACB.

11. 已知两个相似三角形的周长之比是2:3,面积之差是50,则这两个三角形中较小三角形的面积是40.

答案： 40 解析:
∵两个相似三角形的周长之比是2:3,
∴两个相似三角形的面积之比是4:9.设较小三角形的面积是4x,则较大三角形的面积是9x.根据题意得,9x - 4x = 50,解得x = 10.
∴4x = 40,即较小三角形的面积是40.

12. 新考法 探究题 如图,小明在A时测得某树的影长为8m,B时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为____.

答案：
4m 解析:根据题意，如图,作△EFC,树高为CD,且∠ECF = 90°,ED = 2m,FD = 8m.
∵∠E + ∠F = 90°,∠E + ∠ECD = 90°,
∴∠ECD = ∠F.
∴△EDC∽△CDF.
∴$\frac{ED}{DC}=\frac{CD}{FD}$,即$DC^2 = ED\cdot FD = 2×8 = 16(m^2)$.
∴CD = 4m.

13. (2024·云南)如图,AB与CD交于点O,且$AC // BD$.若$\frac{OA+OC+AC}{OB+OD+BD}= \frac{1}{2}$,则$\frac{AC}{BD}= $$\frac{1}{2}$.

答案： $\frac{1}{2}$ 解析:
∵AC//BD,
∴△AOC∽△BOD.
∴$\frac{OA + OC + AC}{OB + OD + BD}=\frac{AC}{BD}$.
∵$\frac{OA + OC + AC}{OB + OD + BD}=\frac{1}{2}$,
∴$\frac{AC}{BD}=\frac{1}{2}$.

14. (2024·宜宾)如图,正五边形ABCDE的边长为4,则这个正五边形的对角线AC的长是____.

答案：
$2\sqrt{5}+2$ 解析:连接BE交AC于点O,如图所示.
∵五边形ABCDE是正五边形,
∴∠CBA = ∠BAE = (5 - 2)×180°÷5 = 108°,BC = AB = AE.
∴∠BCA = ∠BAC = ∠ABE = ∠AEB = (180° - 108°)÷2 = 36°.
∴∠CBO = ∠ABC - ∠ABE = 108° - 36° = 72°.
∴∠BOC = 180° - ∠CBO - ∠BCA = 180° - 72° - 36° = 72°.
∴∠CBO = ∠BOC = 72°.
∴CO = BC = 4.
∵∠BAO = ∠CAB,∠ABO = 36° = ∠BCA,
∴△ABO∽△ACB.
∴$\frac{AB}{AC}=\frac{AO}{AB}$,即$\frac{4}{AC}=\frac{AC - 4}{4}$,解得$AC = 2\sqrt{5}+2$或$AC = 2 - 2\sqrt{5}$(舍去).经检验,$AC = 2\sqrt{5}+2$符合题意.

15. 如图,在平面直角坐标系中,A和C是反比例函数$y= \frac{1}{x}$图像上的两点,以AC为边作等边三角形ABC,反比例函数$y= \frac{k}{x}(x＞0)$的图像恰好过点B,则k的值为____.

答案：
-3 解析:如图,过点A作AM⊥y轴于点M,过点B作BN⊥y轴于点N,连接BO.设A(m,n),则有mn = 1.
∵△ABC是等边三角形,OA = OC,
∴OB⊥AC,$OB=\sqrt{3}OA$.
∵∠AMO = ∠BNO = ∠AOB = 90°,
∴∠AOM + ∠BON = 90°,∠BON + ∠OBN = 90°.
∴∠AOM = ∠OBN.
∴△AMO∽△ONB.
∴$\frac{S_{\triangle AMO}}{S_{\triangle ONB}} = (\frac{OA}{OB})^2=\frac{1}{3}$.
∵$S_{\triangle AMO}=\frac{1}{2}$,
∴$S_{\triangle ONB}=\frac{3}{2}$.
∴$\frac{|k|}{2}=\frac{3}{2}$.
∵k＜0,
∴k = -3.

16. (2024·无锡)如图,在$\triangle ABC$中,$AC= 2,AB= 3$,直线$CM // AB$,E是BC上的动点(端点除外),射线AE交CM于点D.在射线AE上取一点P,使得$AP= 2ED$,作$PQ // AB$,交射线AC于点Q.设$AQ= x,PQ= y$.当$x= y$时,$CD= $2;在点E运动的过程中,y关于x的函数表达式为$y=\frac{3x^2}{8 - 2x}$.

答案： 2 $y=\frac{3x^2}{8 - 2x}$ 解析:
∵CM//AB,PQ//AB,
∴CD//PQ.
∴△APQ∽△ADC.
∴$\frac{AQ}{AC}=\frac{PQ}{CD}$,即$\frac{x}{2}=\frac{y}{CD}$.
∵x = y,
∴CD = 2.
∵△APQ∽△ADC,
∴$\frac{AQ}{AC}=\frac{PQ}{CD}$,即$\frac{x}{2}=\frac{y}{CD}$,整理,得$CD=\frac{2y}{x}$.设DE = t.
∵AP = 2ED,
∴AP = 2t.
∵CM//AB,
∴△CDE∽△BAE.
∴$\frac{CD}{AB}=\frac{DE}{AE}$,即$\frac{\frac{2y}{x}}{3}=\frac{t}{AE}$.整理,得$AE=\frac{3xt}{2y}$.
∴$AD = AE + DE=\frac{3xt}{2y}+t=\frac{t(3x + 2y)}{2y}$.
∵△APQ∽△ADC,
∴$\frac{AQ}{AC}=\frac{AP}{AD}$,即$\frac{x}{2}=\frac{2t}{\frac{t(3x + 2y)}{2y}}$.整理,得$y=\frac{3x^2}{8 - 2x}$.