《2025年通城学典全程测评卷九年级数学全一册苏科版》

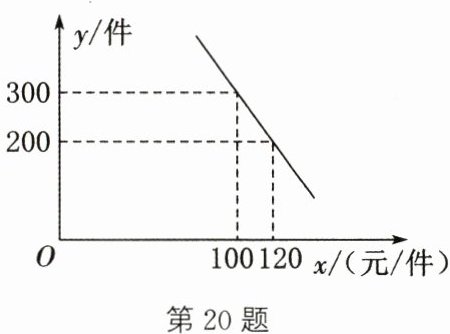
20. (8分)(2024·济宁)某商场以每件80元的价格购进一种商品,在一段时间内,销售量y(单位:件)与销售单价x(单位:元/件)之间是一次函数关系,其部分图像如图所示.
(1)求这段时间内y与x之间的函数表达式.
(2)在这段时间内,若销售单价不低于100元/件,且商场还要完成不少于220件的销售任务,当销售单价为多少时,商场获得的利润最大?最大利润是多少?

答案：
(1)由题意,设一次函数的表达式为y=kx+b.
∵过点(100,300)、(120,200),
∴将(100,300)、(120,200)代入,得$\begin{cases}100k + b =300 \\120k + b =200 \end{cases}$ ,解得$\begin{cases}k=-5 \\b=800 \end{cases}$ ,
∴y与x之间的函数表达式为y=-5x+800
(2)由题意得,$\begin{cases}x≥100 \\-5x + 800≥220 \end{cases}$ ,
∴100≤x≤116.设商场获得的利润为w元,则w=(x - 80)(-5x+800)=-5x²+1200x - 64000=-5(x - 120)²+8000.
∵-5 ＜ 0,100≤x≤116,
∴当x=116时,w=7920.
∴当销售单价为116元/件时,商场获得的利润最大,最大利润是7920元

21. (10分)(2024·江西)如图,一小球从斜坡点O处以一定的方向弹出,不考虑空气阻力,球的飞行路线可以用抛物线$ y = a x ^ { 2 } + b x ( a ＜ 0 ) $刻画,斜坡可以用直线$ y = \frac { 1 } { 4 } x $刻画,小球飞行的水平距离x(米)与小球飞行的高度y(米)之间的变化规律如表:
| x/米 | 0 | 1 | 2 | m | 4 | 5 | 6 | 7 | … |
| y/米 | 0 | $ \frac { 7 } { 2 } $ | 6 | $ \frac { 15 } { 2 } $ | 8 | $ \frac { 15 } { 2 } $ | n | $ \frac { 7 } { 2 } $ | … |
(1)①$ m = $3,$ n = $6;
②小球的落点是A,求点A的坐标.联立得$\begin{cases}y = -\frac{1}{2}x²+4x \\y = \frac{1}{4}x \end{cases}$ ,解得$\begin{cases}x = 0 \\y = 0 \end{cases}$ 或$\begin{cases}x = \frac{15}{2} \\y = \frac{15}{8} \end{cases}$ ,∴点A的坐标是($\frac{15}{2}$,$\frac{15}{8}$)
(2)小球飞行的高度y(米)与飞行时间t(秒)满足关系$ y = - 5 t ^ { 2 } + v t $.
①小球飞行的最大高度为8米;
②求v的值.∵y=-5t²+vt=-5(t - $\frac{v}{10}$)²+$\frac{v²}{20}$ ,∴$\frac{v²}{20}$=8,解得v=4$\sqrt{10}$(负值舍去)

答案：
(1)①3 6 解析:将(2,6)、(4,8)代入y=ax²+bx,得$\begin{cases}4a + 2b =6 \\16a + 4b =8 \end{cases}$ ,解得$\begin{cases}a=-\frac{1}{2} \\b=4 \end{cases}$ ,
∴二次函数的表达式为y=-$\frac{1}{2}$x²+4x.当y=$\frac{15}{2}$时,-$\frac{1}{2}$x²+4x=$\frac{15}{2}$ ,解得x=3或x=5.
∴m=3;当x=6时,y=-$\frac{1}{2}$×6²+4×6=6.
∴n=6.
②联立得$\begin{cases}y = -\frac{1}{2}x²+4x \\y = \frac{1}{4}x \end{cases}$ ,解得$\begin{cases}x = 0 \\y = 0 \end{cases}$ 或$\begin{cases}x = \frac{15}{2} \\y = \frac{15}{8} \end{cases}$ ,
∴点A的坐标是($\frac{15}{2}$,$\frac{15}{8}$)
(2)①8 解析:由题干可知小球飞行的最大高度为8米.
②
∵y=-5t²+vt=-5(t - $\frac{v}{10}$)²+$\frac{v²}{20}$ ,
∴$\frac{v²}{20}$=8,解得v=4$\sqrt{10}$(负值舍去)