《2025年通城学典全程测评卷九年级数学全一册苏科版》

8. (2024·达州)抛物线$ y = - x ^ { 2 } + b x + c $与x轴交于两点,其中一个交点的横坐标大于1,另一个交点的横坐标小于1,则下列结论正确的是 (A)
A.$ b + c ＞ 1 $
B.$ b = 2 $
C.$ b ^ { 2 } + 4 c ＜ 0 $
D.$ c ＜ 0 $

答案： A 解析:
∵抛物线y=-x²+bx+c与x轴交于两点,设这两点的坐标分别为(x₁,0)和(x₂,0),且x₁ ＜ 1,
∴x₁ - 1 ＜ 0,x₂ - 1 ＞ 0.
∴(x₁ - 1)(x₂ - 1) ＜ 0.
∴x₁x₂-(x₁+x₂)+1 ＜ 0.由根与系数的关系可得,-c - b+1 ＜ 0.
∴b+c ＞ 1.

9. 若函数$ y = ( m - 3 ) x ^ { m ^ { 2 } - 3 m + 2 } $是关于x的二次函数,则m的值是0.

答案： 0 解析:
∵函数y=(m - 3)x^{m² - 3m + 2}是关于x的二次函数,
∴m² - 3m + 2=2且m - 3≠0,解得m=0.

10. (2024·长春)若抛物线$ y = x ^ { 2 } - x + c $(c是常数)与x轴没有交点,则c的取值范围是c ＞ $\frac{1}{4}$.

答案： c ＞ $\frac{1}{4}$ 解析:
∵抛物线y=x² - x+c(c是常数)与x轴没有交点,
∴b² - 4ac=1 - 4c ＜ 0.
∴c ＞ $\frac{1}{4}$.

11. (2024·泰安)如图,小明的父亲想用长为60米的栅栏,再借助房屋的外墙围成一个矩形的菜园.已知房屋的外墙长40米,则可围成的菜园的最大面积是450平方米.

答案： 450 解析:由题意,设垂直于外墙的边长为x米,则平行于外墙的边长为(60 - 2x)米,又
∵外墙长40米,
∴0 ＜ 60 - 2x≤40.
∴10≤x ＜ 30.
∵菜园的面积=x(60 - 2x)=-2x²+60x=-2(x - 15)²+450.
∴当x=15时,y=450,即可围成的菜园的最大面积是450平方米.

12. (2024·内江)已知二次函数$ y = x ^ { 2 } - 2 x + 1 $的图像向左平移两个单位长度得到抛物线C,点$ P ( 2, y _ { 1 } ) $、$ Q ( 3, y _ { 2 } ) $在抛物线C上,则$ y _ { 1 } $＜$ y _ { 2 } $(填“＞”“＜”或“=”).

答案： ＜ 解析:
∵y=x² - 2x+1=(x - 1)²,
∴二次函数y=x² - 2x+1的图像向左平移两个单位长度得到的抛物线C对应的函数表达式为y=(x - 1+2)²,即y=(x + 1)².
∴抛物线C开口向上,对称轴为直线x=-1.
∵点P(2,y₁)、Q(3,y₂)在抛物线C上,且-1 ＜ 2 ＜ 3,
∴y₁ ＜ y₂.

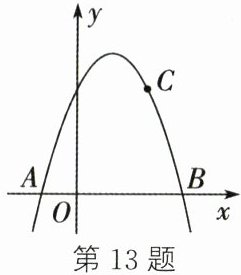
13. (2024·辽宁)如图,在平面直角坐标系中,抛物线$ y = a x ^ { 2 } + b x + 3 $与x轴相交于点A、B,点B的坐标为$ ( 3, 0 ) $,若点$ C ( 2, 3 ) $在抛物线上,则AB的长为4.

答案： 4 解析:
∵抛物线y=ax²+bx+3过点B(3,0)、C(2,3),
∴$\begin{cases}9a + 3b + 3 =0 \\4a + 2b + 3 =3 \end{cases}$ ,解得$\begin{cases}a=-1 \\b=2 \end{cases}$ ,
∴抛物线对应的函数表达式为y=-x²+2x+3.
∴抛物线的对称轴是直线x=$\frac{2}{2×(-1)}$=1.
∵抛物线与x轴的一个交点为B(3,0),
∴它与x轴的另一个交点为A(-1,0).
∴AB=3 - (-1)=4.

14. 新考法 新定义题(2024·上海)对于一个二次函数$ y = a ( x - m ) ^ { 2 } + k ( a \neq 0 ) $的图像中存在一点$ P ( x ^ { \prime }, y ^ { \prime } ) ,$使得$ x ^ { \prime } - m = y ^ { \prime } - k \neq 0 ,$则称 2 |$ x ^ { \prime } - m $| 为该抛物线的“开口大小”,那么抛物线$ y = - \frac { 1 } { 2 } x ^ { 2 } + \frac { 1 } { 3 } x + 3 $的“开口大小”为4.

答案： 4 解析:
∵抛物线y=-$\frac{1}{2}$x²+$\frac{1}{3}$x+3=-$\frac{1}{2}$(x - $\frac{1}{3}$)²+$\frac{55}{18}$ ,
∴x' - $\frac{1}{3}$=-$\frac{1}{2}$(x' - $\frac{1}{3}$)²+$\frac{55}{18}$-$\frac{55}{18}$≠0.
∴x' - $\frac{1}{3}$=-2.
∴抛物线y=-$\frac{1}{2}$x²+$\frac{1}{3}$x+3的“开口大小”为2|x' - $\frac{1}{3}$|=2×|-2|=4.

15. (2024·甘肃)如图①所示为一个停车棚,其棚顶的横截面可以看作是抛物线的一部分.棚顶的竖直高度y(单位:m)与距离停车棚支柱AO的水平距离x(单位:m)近似满足函数关系$ y = - 0.02 x ^ { 2 } + 0.3 x + 1.6 $,其图像的一部分如图②所示,点$ B ( 6, 2.68 ) $在图像上.一辆厢式货车需在该停车棚下避雨,若货车截面看作长CD为4m、高DE为1.8m的矩形,则该货车能完全停到停车棚内(填“能”或“不能”).

答案： 能 解析:
∵CD=4 m,B(6,2.68),
∴6 - 4=2.在y=-0.02x²+0.3x+1.6中,当x=2时,y=-0.02×2²+0.3×2+1.6=2.12.
∵2.12 ＞ 1.8,
∴货车能完全停到停车棚内.

16. (2024·无锡)经过点$ ( 0, 3 ) $且平行于x轴的直线与二次函数$ y = \frac { 1 } { 2 } x ^ { 2 } - \frac { 3 } { 2 } x + 1 $的图像交于A、B两点(点A在点B的左侧),将图像向右平移$ m ( m ＞ 0 ) $个单位长度后,所得的二次函数的图像与x轴交于C、D两点(点C在点D的左侧),若在x轴上存在点E使得四边形ACEB为菱形,则m的值为____2.

答案： 2 解析:当y=0时,$\frac{1}{2}$x² - $\frac{3}{2}$x+1=0,解得x₁=1,x₂=2.
∴抛物线y=$\frac{1}{2}$x² - $\frac{3}{2}$x+1与x轴交点坐标为(1,0)、(2,0).
∵抛物线y=$\frac{1}{2}$x² - $\frac{3}{2}$x+1向右平移m(m ＞ 0)个单位长度后,所得的二次函数的图像与x轴交于C、D两点(点C在点D的左侧),
∴C(1 + m,0).当y=3时,$\frac{1}{2}$x² - $\frac{3}{2}$x+1=3,解得x₁=-1,x₂=4.
∴A(-1,3)、B(4,3).
∴AB=5.
∵四边形ACEB为菱形,
∴AC=AB=5.
∴(1 + m+1)²+3²=5²,解得m₁=2,m₂=-6(舍去),即m的值为2.