《2025年通城学典全程测评卷九年级数学全一册苏科版》

9. (2024·盐城阜宁期中)数据-1、0、1、2、5、8的极差是9.

答案： 9 解析:根据题意可知,这组数据中最大的是8,最小的是 -1,
∴这组数据的极差为8 - (-1) = 8 + 1 = 9.

10. 若a、b是方程$x^{2} - x - 2025 = 0$的两根,则$2a + 2b + 2024 = $2026.

答案： 2026 解析:
∵a、b是方程x² - x - 2025 = 0的两根,
∴a + b = 1.
∴2a + 2b + 2024 = 2(a + b) + 2024 = 2×1 + 2024 = 2026.

11. (2024·盐城盐都期中)如图所示为用相同的正方形砖铺成的地面,一宝物藏在其中某一块砖的下面.宝物在涂色区域的概率是$\frac{1}{2}$.

答案： $\frac{1}{2}$ 解析:题图中共16块砖,其中涂色的砖有8块,
∴宝物藏在涂色区域的概率是$\frac{8}{16}$ = $\frac{1}{2}$.

12. (2024·盐城响水期中)若圆锥的底面圆的半径为2cm,母线长是5cm,则它的侧面展开图的面积为10π$cm^{2}$.

答案： 10π 解析:根据题意,得圆锥的侧面展开图的面积 = $\frac{1}{2}$×2π×2×5 = 10π(cm²).

13. 如图,正六边形ABCDEF内接于$\odot O$,$OA = 1$,则AB的长为1.

答案： 1 解析:
∵正六边形ABCDEF内接于⊙O,
∴∠AOB = $\frac{1}{6}$×360° = 60°.
∵OA = OB,
∴△AOB是等边三角形.
∴AB = OA = 1.

14. (2024·盐城亭湖期中)关于x的方程$(k + 1)x^{2} - 2x + 1 = 0$有实数根,则k的取值范围是k≤0.

答案： k≤0 解析:依题意,得当k + 1 = 0,即k = -1时,方程有实根;当k≠ -1时,依题意,得b² - 4ac = (-2)² - 4(k + 1)×1≥0,解得k≤0.

15. (2024·高邮期中)关于x的方程$a(x + m)^{2} + b = 0$的根是-2、1(a、m、b均为常数,$a\neq 0$),则方程$a(x + m + 2)^{2} + b = 0$的根是-4、-1.

答案： -4、-1 解析:令y = x + 2,得a(y + m)² + b = 0.由题意,得y₁ = -2、y₂ = 1.
∴x + 2 = -2或x + 2 = 1,解得x = -4或x = -1.

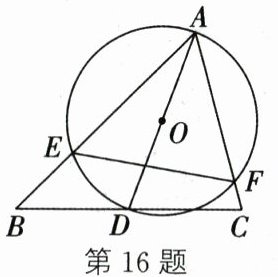
16. (2024·盐城盐都期中)如图,$\angle BAC = 60^{\circ}$,$\angle ABC = 45^{\circ}$,$AB = 6\sqrt{2}$,D是线段BC上的一个动点,以AD为直径画$\odot O$分别交AB、AC于点E、F,连接EF,则线段EF长度的最小值为____.

答案：
3$\sqrt{3}$ 解析:如图,连接OE、OF,作OM⊥EF于点M,作AN⊥BC于点N.
∵∠EOF = 2∠BAC = 2×60° = 120°,OE = OF,OM⊥EF,
∴∠OEM = 30°,EM = FM.在Rt△OEM中,OM = $\frac{1}{2}$OE,EM = $\frac{\sqrt{3}}{2}$OE,
∴EF = 2EM = $\sqrt{3}$OE.当OE的长度最小时,EF的长度也最小,即此时圆的直径最小.
∵AD的长度的最小值为AN的长度,且易得AN = $\frac{\sqrt{2}}{2}$AB = 6,
∴OE的长度的最小值为3.
∴EF长度的最小值为$\sqrt{3}$×3 = 3$\sqrt{3}$.

17. (8分)(2024·东台期中)解方程:
(1)$x^{2} - 4x - 1 = 0$;
(2)$x(x - 1) + 2 = 2x$.

答案：
(1)x² - 4x - 1 = 0,x² - 4x = 1,x² - 4x + 4 = 1 + 4,(x - 2)² = 5,x - 2 = ±$\sqrt{5}$,x₁ = 2 + $\sqrt{5}$,x₂ = 2 - $\sqrt{5}$
(2)x(x - 1) + 2 = 2x,x(x - 1) + 2 - 2x = 0,x(x - 1) - 2(x - 1) = 0,(x - 2)(x - 1) = 0,x₁ = 2,x₂ = 1