《2025年通城学典全程测评卷九年级数学全一册苏科版》

1. 学校组织了“安全知识”小竞赛,某班的5名同学的成绩(单位:分)如下:90、93、92、95、95.这组数据的中位数是 (C)
A.90
B.92
C.93
D.95

答案： C 解析:将这5个数据从小到大排列为90、92、93、95、95,
∴这组数据的中位数为93.

2. 在$\triangle ABC$中,若$\angle C= 90^{\circ}$,$AC= 3$,$AB= 5$,则$\sin B$的值是 (C)
A.$\frac{3}{4}$
B.$\frac{4}{3}$
C.$\frac{3}{5}$
D.$\frac{4}{5}$

答案： C 解析:
∵在△ABC中,∠C=90°,AC=3,AB=5,
∴sinB=$\frac{AC}{AB}$=$\frac{3}{5}$.

3. 如图,$\odot O上有三点A$、$B$、$C$,连接$AB$、$AC$、$OB$、$OC$.若$\angle A= 36^{\circ}$,则$\angle BOC$的度数是 (A)
A.$72^{\circ}$
B.$54^{\circ}$
C.$36^{\circ}$
D.$18^{\circ}$

答案： A 解析:
∵∠A=$\frac{1}{2}$∠BOC,∠A=36°,
∴∠BOC=2∠A=2×36°=72°.

4. 对于二次函数$y= (x-2)^{2}+1$的图像,下列说法正确的是 (D)
A.对称轴是直线$x= -2$
B.开口向下
C.与$x$轴有两个交点
D.顶点坐标是$(2,1)$

答案： D 解析:
∵y=(x−2)²+1,
∴抛物线的开口向上,对称轴为直线x=2,顶点坐标为(2,1).
∴选项A和选项B不符合题意,选项D符合题意.令y=0,得(x−2)²+1=0,方程没有实数根,
∴抛物线y=(x−2)²+1与x轴没有交点.
∴选项C不符合题意.

5. 关于$x的一元二次方程x^{2}+4x+m= 0$有两个不相等的实数根,则$m$的值可能是 (D)
A.9
B.6
C.4
D.$-1$

答案： D 解析:
∵关于x的一元二次方程x²+4x+m=0有两个不相等的实数根，
∴b²−4ac=4²−4m＞0,解得m＜4.

6. 四个半径为5的等圆与直线$l$的位置关系如图所示,若某个圆上的点到直线$l$的最大距离为8,则这个圆是 (C)
A.$\odot O_{1}$
B.$\odot O_{2}$
C.$\odot O_{3}$
D.$\odot O_{4}$

答案： C 解析:⊙O₁与直线l相切,因此⊙O₁上的点到直线l的最大距离为10,不符合题意;⊙O₂的圆心在直线l上,因此⊙O₂上的点到直线l的最大距离为5,不符合题意;⊙O₃与直线l相交,因此⊙O₃上的点到直线l的最大距离可能为8,符合题意;⊙O₄与直线l相离,因此⊙O₄上的点到直线l的最大距离大于10,不符合题意.

7. 在平面直角坐标系中,抛物线$y= 4(x-2)^{2}+m经过A(3,a)$、$B(0,b)$、$C(1,c)$三点,则$a$、$b$、$c$的大小关系是 (D)
A.$b＜c＜a$
B.$a＜c＜b$
C.$b＜a= c$
D.$a= c＜b$

答案： D 解析:抛物线的对称轴为直线x=2,
∴点A(3,a)关于对称轴的对称点为(1,a).
∵4＞0,
∴当x＜2时,y随x的增大而减小.
∴a=c＜b.

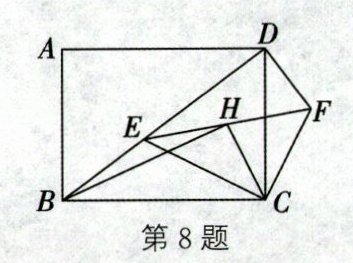
8. 如图,在矩形$ABCD$中,$AB= 6$,$BC= 8$,点$E在矩形的对角线BD$上,连接$CE$.过点$C作CF\perp CE$,过点$D作DF\perp DE$,$DF与CF相交于点F$,连接$EF$,$H是线段EF$的中点,连接$CH和BH$.有下列结论:①$\triangle BCE\backsim\triangle DCF$,且相似比为$4:3$;②点$D$、$E$、$C$、$F$在同一个圆上;③$\triangle BCH的面积随线段BE$长度的增大而增大;④当$\triangle DEF$面积大于9时,线段$BE长的取值范围是4＜BE＜6$.其中,正确的个数为 ( )B

A.4
B.3
C.2
D.1

答案： B 解析:①如图,
∵四边形ABCD是矩形,
∴∠A=∠ADC=∠BCD=90°,AD//BC,DC=AB=6,AD=BC=8.
∴BD=$\sqrt{BC²+CD²}$=$\sqrt{6²+8²}$=10,∠2+∠CDE=90°.
∵CF⊥CE,DF⊥DE,
∴∠ECF=∠EDF=90°.
∴∠1+∠CDE=90°.
∴∠1=∠2.
∵AD//BC,
∴∠EBC=∠2.
∴∠EBC=∠1.
∵∠4+∠DCE=∠BCD=90°,∠3+∠ECD=∠ECF=90°,
∴∠4=∠3.
∴△BCE∽△DCF.
∴$\frac{BE}{DF}$=$\frac{BC}{DC}$=$\frac{8}{6}$=$\frac{4}{3}$.
∴△BCE∽△DCF,且相似比为4:3,即①正确;②如图,连接DH.
∵∠EDF=∠ECF=90°,H是线段EF的中点,
∴CH=DH=$\frac{1}{2}$EF=EH=FH.
∴点D、E、C、F在同一个圆上,即②正确;③由②,得DH=CH,
∴点H在CD的垂直平分线上.如图,过点H分别作HM⊥CD,HN⊥BC,垂足分别是M、N,则∠HMC=∠HNC=90°.又
∵∠MCN=90°,
∴四边形CMHN是矩形.
∴HN=CM.
∵CH=DH且HM⊥CD,
∴CM=$\frac{1}{2}$CD=$\frac{1}{2}$×6=3.
∴S△BCH=$\frac{1}{2}$BC·HN=$\frac{1}{2}$×8×3=12,即△BCH的面积不随线段BE长度的增大而增大,即③错误;④由①,可知△BCE∽△DCF,且相似比为4:3,
∴设BE=x,则DE=10−x,DF=$\frac{3}{4}$BE=$\frac{3}{4}$x.
∴S△DEF=$\frac{1}{2}$DE·DF=$\frac{1}{2}$·$\frac{3}{4}$x(10−x)=−$\frac{3}{8}$x²+$\frac{15}{4}$x.当△DEF面积大于9,即−$\frac{3}{8}$x²+$\frac{15}{4}$x＞9时,
∵−$\frac{3}{8}$＜0,
∴抛物线开口方向向下.令−$\frac{3}{8}$x²+$\frac{15}{4}$x=9,解得x₁=4,x₂=6.
∴当−$\frac{3}{8}$x²+$\frac{15}{4}$x＞9时,x的取值范围是4＜x＜6,即4＜BE＜6,故④正确.综上所述，正确的有①②④,共3个.