第124页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
1. 1202年数学家斐波那契在《计算之书》中记载了一列数:1、1、2、3、5、…这一列数满足:从第三个数开始,每一个数都等于它的前两个数之和.在这一列数的前2024个数中,奇数的个数为 (
A.676
B.674
C.1348
D.1350
D
)A.676
B.674
C.1348
D.1350
答案:
D解析:这列数如下:1、1、2、3、5、8、13、21、34、…,可以发现每3个数为一组,每一组前2个数为奇数,第3个数为偶数。
∵2024÷3 = 674……2,
∴前2024个数共有674组,且余2个数。
∴奇数有674×2 + 2 = 1350(个)。
∵2024÷3 = 674……2,
∴前2024个数共有674组,且余2个数。
∴奇数有674×2 + 2 = 1350(个)。
2. (2024·镇江)如图,在平面直角坐标系中,过点A(m,0)且垂直于x轴的直线l与反比例函数y= $-\frac{4}{x}$的图像交于点B,将直线l绕点B逆时针旋转45°,所得的直线经过第一、二、四象限,则m的取值范围是 (
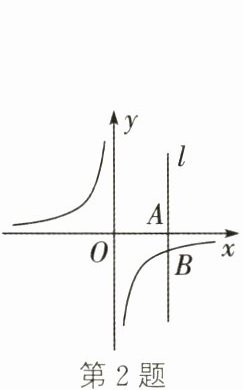
A.m<-2或m>2
B.-2<m<2且m≠0
C.-2<m<0或m>2
D.m<-2或0<m<2
C
)
A.m<-2或m>2
B.-2<m<2且m≠0
C.-2<m<0或m>2
D.m<-2或0<m<2
答案:
C 解析:当点A在原点右侧时,点B的坐标为(m,$-\frac{4}{m}$)。
∵直线l绕点B逆时针旋转45°,
∴所得的直线与直线y = -x平行。设这条直线对应的函数表达式为y = -x + b。
∵这条直线经过第一、二、四象限,
∴b>0。
∵点B在直线y = -x + b上,
∴-m + b = -$\frac{4}{m}$,
∴b = m - $\frac{4}{m}$ = $\frac{m² - 4}{m}$>0。
∵m>0,
∴m² - 4>0,
∴m>2。当点A在原点左侧时,设这条直线对应的函数表达式为y = -x + b',同理,得b' = $\frac{m² - 4}{m}$>0。
∵m<0,
∴m² - 4<0,
∴ - 2<m<2。
∵m<0,
∴ - 2<m<0。
∴m的取值范围是 - 2<m<0或m>2。
∵直线l绕点B逆时针旋转45°,
∴所得的直线与直线y = -x平行。设这条直线对应的函数表达式为y = -x + b。
∵这条直线经过第一、二、四象限,
∴b>0。
∵点B在直线y = -x + b上,
∴-m + b = -$\frac{4}{m}$,
∴b = m - $\frac{4}{m}$ = $\frac{m² - 4}{m}$>0。
∵m>0,
∴m² - 4>0,
∴m>2。当点A在原点左侧时,设这条直线对应的函数表达式为y = -x + b',同理,得b' = $\frac{m² - 4}{m}$>0。
∵m<0,
∴m² - 4<0,
∴ - 2<m<2。
∵m<0,
∴ - 2<m<0。
∴m的取值范围是 - 2<m<0或m>2。
3. 新考向 数学文化 (2024·河北)“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图①所示的“表格算法”,图①表示132×23,运算结果为3036.图②表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图②中现有数据进行推断,正确的是 (
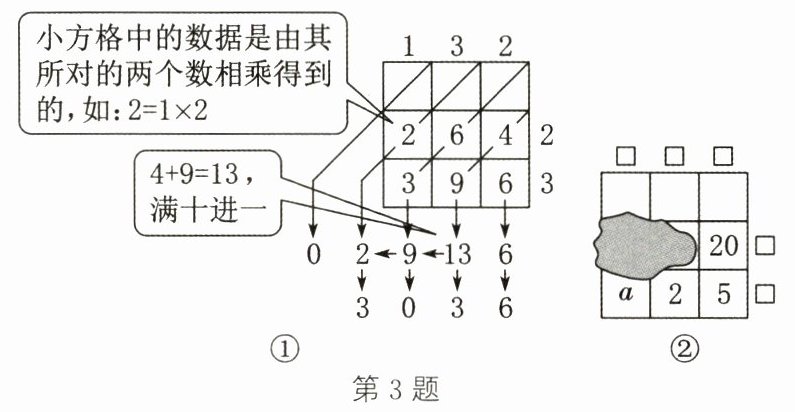
A.“20”左边的数是16
B.“20”右边的“□”表示5
C.运算结果小于6000
D.运算结果可以表示为4100a+1025
D
)
A.“20”左边的数是16
B.“20”右边的“□”表示5
C.运算结果小于6000
D.运算结果可以表示为4100a+1025
答案:
D 解析:设一个三位数与一个两位数分别为100x + 10y + z和10m + n。如图①,由题意得,mz = 20,nz = 5,ny = 2,nx = a,
∴$\frac{mz}{nz}$ = 4,即m = 4n。
∴当n = 2,y = 1时,z = 2.5不是正整数,不符合题意,舍去;当n = 1,y = 2时,m = 4,z = 5,x = a,如图②所示。
∴A:“20”左边的数是2×4 = 8,本选项不符合题意;B:“20”右边的“□”表示4,本选项不符合题意;
∵a上面的数应为4a,如图③所示。
∴运算结果可以表示为1000(4a + 1) + 100a + 20 + 5 = 4100a + 1025。
∴D选项符合题意。当a = 2时,计算的结果大于6000,C选项不符合题意。
∴$\frac{mz}{nz}$ = 4,即m = 4n。
∴当n = 2,y = 1时,z = 2.5不是正整数,不符合题意,舍去;当n = 1,y = 2时,m = 4,z = 5,x = a,如图②所示。
∴A:“20”左边的数是2×4 = 8,本选项不符合题意;B:“20”右边的“□”表示4,本选项不符合题意;
∵a上面的数应为4a,如图③所示。
∴运算结果可以表示为1000(4a + 1) + 100a + 20 + 5 = 4100a + 1025。
∴D选项符合题意。当a = 2时,计算的结果大于6000,C选项不符合题意。
4. (2024·淮安)如图,在□ABCD中,AB= 2,BC= 3,∠B= 60°,P是BC边上的动点(BP>1),将△ABP沿AP折叠得△AB'P,射线PB'与射线AD交于点E.下列说法不正确的是 (
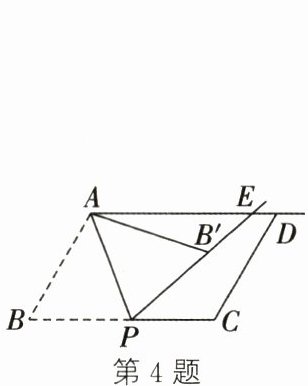
A.当AB'⊥AB时,B'A= B'E
B.当点B'落在AD上时,四边形ABPB'是菱形
C.在点P运动的过程中,线段AE的最小值为2
D.若连接BB',则四边形ABPB'的面积始终等于$\frac{1}{2}$AP·BB'
C
)
A.当AB'⊥AB时,B'A= B'E
B.当点B'落在AD上时,四边形ABPB'是菱形
C.在点P运动的过程中,线段AE的最小值为2
D.若连接BB',则四边形ABPB'的面积始终等于$\frac{1}{2}$AP·BB'
答案:
C 解析:A选项:如图①。
∵AB'⊥AB,
∴∠BAB' = 90°。
∵折叠,
∴∠BAP = ∠B'AP = 45°,∠B = ∠AB'P = 60°。
∵四边形ABCD是平行四边形,
∴AD//BC。
∴∠BAD = 120°。
∴∠B'AD = ∠BAD - ∠BAB' = 30°。
∴∠AEB' = ∠AB'P - ∠B'AD = 30°。
∴∠B'AD = ∠AEB'。
∴B'A = B'E,故选项A正确,不合题意;B选项:如图②,当点B'落在AD上时,点E和点B'重合。
∵四边形ABCD是平行四边形,
∴AD//BC。
∴∠BAD = 120°。
∵折叠,
∴∠BAP = ∠B'AP = 60°,AB = AB',PB = PB'。
∴△ABP是等边三角形,
∴AB = BP = B'P = AB'。
∴四边形ABPB'是菱形,故选项B正确,不合题意;C选项:如图③,当点P靠近点C时,点B'在四边形外部,此时∠AEB'>90°。
∴AE<AB' = 2,故选项C错误,符合题意;D选项:如图④,连接BB'交AP于点O。
∵折叠,且AP是折痕,
∴AP垂直平分BB'。
∴S四边形ABPB' = S△ABP + S△AB'P = $\frac{1}{2}$AP·OB + $\frac{1}{2}$AP·OB' = $\frac{1}{2}$AP·BB',故选项D正确,不合题意。
∵AB'⊥AB,
∴∠BAB' = 90°。
∵折叠,
∴∠BAP = ∠B'AP = 45°,∠B = ∠AB'P = 60°。
∵四边形ABCD是平行四边形,
∴AD//BC。
∴∠BAD = 120°。
∴∠B'AD = ∠BAD - ∠BAB' = 30°。
∴∠AEB' = ∠AB'P - ∠B'AD = 30°。
∴∠B'AD = ∠AEB'。
∴B'A = B'E,故选项A正确,不合题意;B选项:如图②,当点B'落在AD上时,点E和点B'重合。
∵四边形ABCD是平行四边形,
∴AD//BC。
∴∠BAD = 120°。
∵折叠,
∴∠BAP = ∠B'AP = 60°,AB = AB',PB = PB'。
∴△ABP是等边三角形,
∴AB = BP = B'P = AB'。
∴四边形ABPB'是菱形,故选项B正确,不合题意;C选项:如图③,当点P靠近点C时,点B'在四边形外部,此时∠AEB'>90°。
∴AE<AB' = 2,故选项C错误,符合题意;D选项:如图④,连接BB'交AP于点O。
∵折叠,且AP是折痕,
∴AP垂直平分BB'。
∴S四边形ABPB' = S△ABP + S△AB'P = $\frac{1}{2}$AP·OB + $\frac{1}{2}$AP·OB' = $\frac{1}{2}$AP·BB',故选项D正确,不合题意。
查看更多完整答案,请扫码查看


