《2025年通城学典全程测评卷九年级数学全一册苏科版》

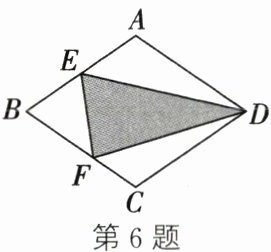
6. (2024·广东)如图,菱形ABCD的面积为24,E是AB的中点,F是BC上的动点.若$\triangle BEF$的面积为4,则图中涂色部分的面积为____.

答案：
10 解析:如图,连接BD.
∵ E是AB的中点,
∴ $S_{\triangle AED}=\frac{1}{2}S_{\triangle ABD}=\frac{1}{4}S_{菱形ABCD}=6$.连接EC.同理,可得$S_{\triangle BEC}=S_{\triangle AED}=6$.
∵ $S_{\triangle BEF}=4$,
∴ $S_{\triangle BEF}=\frac{2}{3}S_{\triangle BEC}$.
∴ FC=$\frac{1}{3}BC$.
∴ $S_{\triangle DFC}=\frac{1}{3}S_{\triangle BCD}=\frac{1}{6}S_{菱形ABCD}=4$.
∴ $S_{涂色}=S_{菱形ABCD}-S_{\triangle AED}-S_{\triangle BEF}-S_{\triangle DFC}=24-6-4-4=10$.

7. 某公园广场的地面由形状、大小完全相同的一种地砖密铺(无空隙、不重叠)而成,铺设方式如图①所示.图②是其中一块地砖的示意图及其部分尺寸,$AB= EF,CD= GH,BC= FG,BC// FG,AB// CD// HG// FE$.结合图①、图②的信息,可求得BC的长是____dm.

答案：
5.8 解析:如图,作CM⊥AB.设AB=a dm,CD=b dm,由图可知,GF=BC=AB+CD,DN=7-3=4(dm),四边形CDNM是矩形,则MN=CD=b dm,$\angle BMC=90^{\circ}$.
∴ BM=10-AB-MN=[10-(a+b)]dm.
∵ $CM^{2}+BM^{2}=BC^{2}$,
∴ $4^{2}+[10-(a+b)]^{2}=(a+b)^{2}$.
∴ a+b=5.8.
∴ BC=5.8 dm.

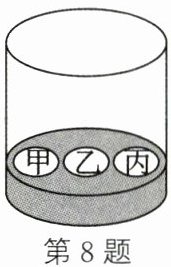
8. (2024·宜宾)如图所示为一个圆柱形容器,其底部有三个完全相同的小孔槽,分别命名为甲槽、乙槽、丙槽.有大小质地完全相同的三个小球,每个小球标有从1至9中选取的一个数字,且每个小球所标数字互不相同.作如下操作:将这三个小球放入容器中,摇动容器使这三个小球全部落入不同的小孔槽(每个小孔槽只能容下一个小球),取出小球记录下各小孔槽的计分(分数为落入该小孔槽小球上所标的数字),完成第一次操作.再重复以上操作两次.已知甲槽、乙槽、丙槽三次操作计分之和分别为20分、10分、9分,其中第一次操作计分最高的是乙槽,则第二次操作计分最低的是____(填"甲槽""乙槽"或"丙槽").


乙槽

答案： 乙槽 解析:
∵ 三次操作相同,且总得分是20+10+9=39(分),
∴ 一次操作的总分,即三个小球数字之和为39÷3=13.有以下情况:①1、3、9;②1、4、8;③1、5、7;④2、3、8;⑤2、4、7;⑥2、5、6;⑦3、4、6.其中只有1、4、8这一组能同时满足三个数字组合相加得20、10、9.4+8+8=20(甲槽);8+1+1=10(乙槽);1+4+4=9(丙槽).
∴ 第一次操作甲槽、乙槽、丙槽的分数分别为4分、8分、1分;第二次操作甲槽、乙槽、丙槽的分数分别为8分、1分、4分;第三次操作甲槽、乙槽、丙槽的分数分别为8分、1分、4分.
∴ 第二次操作计分最低的是乙槽.

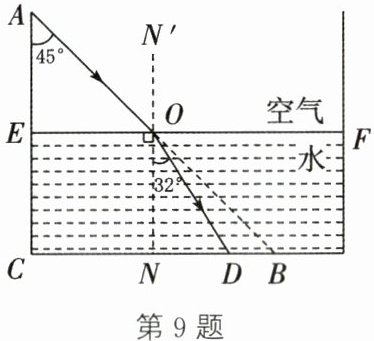
9. (15分)第一步:将长方体空水槽放置在水平桌面上,一束光线从水槽边沿A处投射到底部B处,入射光线与水槽内壁AC的夹角为$∠A$;第二步:向水槽注水,水面上升到AC的中点E处时,停止注水(直线$NN'$为法线,AO为入射光线,OD为折射光线).如图,点A、B、C、D、E、F、O、N、$N'$在同一平面内,测得$AC= 20cm,∠A= 45^{\circ }$,折射角$∠DON= 32^{\circ }$.根据以上实验操作和测量的数据,解答问题(参考数据:$sin32^{\circ }\approx 0.53,cos32^{\circ }\approx 0.85,tan32^{\circ }\approx 0.62$).求:
(1) BC的长;
(2) 点B、D之间的距离(结果精确到0.1 cm).

答案：
(1)在Rt△ABC中,$\angle A=45^{\circ}$,
∴ $\angle B=45^{\circ}$.
∴ BC=AC=20 cm
(2)由题可知ON=EC=$\frac{1}{2}AC=10$ cm.
∴ 易得NB=ON=10 cm.又
∵ $\angle DON=32^{\circ}$,
∴ DN=ON·tan$\angle DON=10·tan32^{\circ}\approx10×0.62=6.2$(cm).
∴ BD=BN-DN=10-6.2=3.8(cm)

10. (20分)(2024·巴中)
(1) 平行四边形和梯形都可以剪开拼成一个矩形,拼接示意图如图①②所示.在图②中,四边形ABCD为梯形,$AB// CD$,E、F分别是AD、BC边上的点.经过剪拼,四边形GHIJK为矩形,则$\triangle EDK\cong$____.
(2) 探究将任意一个四边形剪开拼成一个平行四边形,拼接示意图如图③④⑤所示.在图⑤中,E、F、G、H是四边形ABCD边上的点.OJKL是拼接之后形成的四边形.
① 通过操作得出:AE与EB的比值为____.
② 证明:四边形OJKL为平行四边形.
(3) 任意一个四边形能不能剪开拼成一个矩形? 若能,请将四边形ABCD剪成4块,按图⑤所示的方式补全图⑥,并简单说明剪开和拼接的过程;若不能,请说明理由.

答案：

(1)△EAG 解析:
∵ AB//CD,
∴ $\angle GAE=\angle D$.由题意,得E为AD的中点,
∴ EA=ED.
∵ $\angle AEG=\angle DEK$,
∴ △EDK≌△EAG.
(2)①1 解析:如图①,由操作知,E为AB的中点.
∵ 将四边形EBFO绕点E旋转180°得到四边形EAQL,
∴ AE=BE.
∴ $\frac{AE}{BE}=1$.
②如图①,由题意得,E、F、G、H分别是AB、BC、CD、DA的中点,将四边形EBFO绕点E旋转180°得到四边形EAQL,将四边形OHDG绕点H旋转180°得到四边形JHAP,将四边形OGCF放在左上方,
∴ AQ=BF=CF,AP=DG=CG,$\angle BFO=\angle AQL$.
∵ $\angle DAB+\angle B+\angle C+\angle D=360^{\circ}$,$\angle QAE=\angle B$,$\angle PAH=\angle D$,$\angle DAB+\angle QAE+\angle PAH+\angle PAQ=360^{\circ}$,
∴ $\angle PAQ=\angle C$.
∵ $\angle BFO+\angle CFO=180^{\circ}$,
∴ $\angle AQL+\angle AQK=180^{\circ}$.
∴ K、Q、L三点共线.同理K、P、J三点共线.由操作得$\angle 1=\angle L$,$\angle 3=\angle J$.
∵ $\angle 1+\angle 2=180^{\circ}$,$\angle 2+\angle 3=180^{\circ}$,
∴ $\angle 2+\angle L=180^{\circ}$,$\angle 2+\angle J=180^{\circ}$.
∴ OJ//KL,OL//KJ.
∴ 四边形OJKL为平行四边形
(3)能 如图②,分别取AB、BC、CD、DA的中点E、H、G、F,连接FH,过点E、点G分别作EM⊥FH,GN⊥FH,垂足分别为M、N,将四边形EBHM绕点E旋转180°至四边形EAH'M',将四边形FDGN绕点F旋转180°至四边形FAG'N',将四边形NGCH放在左上方,使得点C与点A重合,CG与AG'重合,CH与AH'重合,点N的对应点为N'',则四边形MM'N''N'即为所求矩形.由操作得,$\angle 1=\angle 4$,$\angle 2=\angle 3$.
∵ $\angle 1+\angle 2=180^{\circ}$,
∴ $\angle 3+\angle 4=180^{\circ}$.
∴ N''、H'、M'三点共线.同理N'、G'、N''三点共线.
∵ $\angle N'=\angle EMF=\angle M'=90^{\circ}$,
∴ 四边形MM'N''N'为矩形.如图③,连接AC、EF、FG、GH、EH.
∵ E、H为BA、BC的中点,
∴ EH//AC,EH=$\frac{1}{2}AC$.同理FG//AC,FG=$\frac{1}{2}AC$.
∴ FG//EH,FG=EH.
∴ $\angle EHM=\angle GFN$.
∵ $\angle EMF=\angle GNH=90^{\circ}$,
∴ △EHM≌△GFN.
∴ EM=GN,MH=NF,
∴ FM=NH.由操作得,AH'=BH,而BH=CH,
∴ AH'=CH.同理,AG'=CG.
∵ $\angle BAD+\angle D+\angle BCD+\angle B=360^{\circ}$,$\angle D=\angle G'AF$,$\angle B=\angle H'AE$,$\angle BAD+\angle H'AE+\angle G'AF+\angle H'AG'=360^{\circ}$,
∴ $\angle H'AG'=\angle C$.
∵ 四边形MM'N''N'为矩形,
∴ N'N''=MM',N''M'=N'M.
∴ N'F+FM=H'M'+H'N''.
∴ MF+NF=MF+MH=M'H'+N''H'.
∴ NH=N''H'.同理NG=N''G'.
∴ 四边形NGCH能放在左上方.
∴ 按照以上操作可以拼成一个矩形