第121页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
1. (2024·南京)某商场促销方案规定:单笔消费金额每满100元立减10元.例如,单笔消费金额为208元时,立减20元.甲在该商场单笔购买2件A商品,立减了20元;乙在该商场单笔购买2件A商品与1件B商品,立减了30元.若B商品的单价是整数元,则它的单价最小是 (
A.1元
B.99元
C.101元
D.199元
A
)A.1元
B.99元
C.101元
D.199元
答案:
A 解析:
∵ 每满100元立减10元,立减了20元说明消费金额满2个100元.
∴ 2件A商品的原价满足200≤2A<300.
∵ 乙在该商场单笔购买2件A商品与1件B商品,立减了30元,说明消费金额满3个100元,
∴ 2件A商品与1件B商品的原价满足300≤2A+B<400.当299≤2A<300时,B的单价最小,为1元.
∵ 每满100元立减10元,立减了20元说明消费金额满2个100元.
∴ 2件A商品的原价满足200≤2A<300.
∵ 乙在该商场单笔购买2件A商品与1件B商品,立减了30元,说明消费金额满3个100元,
∴ 2件A商品与1件B商品的原价满足300≤2A+B<400.当299≤2A<300时,B的单价最小,为1元.
2. (2024·徐州)小明行走的速度与时间的函数关系如图所示,下列情境与之较为相符的是 (
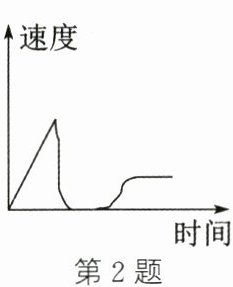
A.小明坐在门口,然后跑去看邻居家的小狗,随后坐着逗小狗玩
B.小明攀岩至高处,然后顺着杆子滑下来,随后躺在沙地上休息
C.小明跑去接电话,然后坐下来电话聊天,随后步行至另一个房间
D.小明步行去朋友家,敲门发现朋友不在家,随后步行回家
C
)
A.小明坐在门口,然后跑去看邻居家的小狗,随后坐着逗小狗玩
B.小明攀岩至高处,然后顺着杆子滑下来,随后躺在沙地上休息
C.小明跑去接电话,然后坐下来电话聊天,随后步行至另一个房间
D.小明步行去朋友家,敲门发现朋友不在家,随后步行回家
答案:
C 解析:由图像,可知速度先随时间的增大而增大,然后直接降为0,过段时间速度增大,然后匀速行驶,在选项C中,小明跑去接电话,然后坐下来电话聊天,随后步行至另一个房间,符合题意.
3. (2024·淮安)如图,用9张直角三角形纸片拼成一个类似海螺的图形,其中每一个直角三角形都有一条直角边长为1.记这个图形的周长(实线部分)为l,则下列整数与l最接近的是 (
A.14
B.13
C.12
D.11
B
)A.14
B.13
C.12
D.11
答案:
B 解析:第一个三角形的斜边长=$\sqrt{1^{2}+1^{2}}$,第二个三角形的斜边长=$\sqrt{1^{2}+(\sqrt{2})^{2}}=\sqrt{3}$……第九个三角形的斜边长=$\sqrt{1^{2}+(\sqrt{9})^{2}}=\sqrt{10}$,
∴ 这个图形的周长=1+1×9+$\sqrt{10}$=10+$\sqrt{10}$.
∵ 与$\sqrt{10}$最接近的整数是3,
∴ 与10+$\sqrt{10}$最接近的整数是13.
∴ 这个图形的周长=1+1×9+$\sqrt{10}$=10+$\sqrt{10}$.
∵ 与$\sqrt{10}$最接近的整数是3,
∴ 与10+$\sqrt{10}$最接近的整数是13.
4. (2024·武汉)如图,小好同学用计算机软件绘制函数$y= x^{3}-3x^{2}+3x-1$的图像,发现它关于点$(1,0)$中心对称.若点$A_{1}(0.1,y_{1})$、$A_{2}(0.2,y_{2})$、$A_{3}(0.3,y_{3})$、…、$A_{19}(1.9,y_{19})$、$A_{20}(2,y_{20})$都在函数图像上,这20个点的横坐标从0.1开始依次增加0.1,则$y_{1}+y_{2}+y_{3}+... +y_{19}+y_{20}$的值是(
A.-1
B.-0.729
C.0
D.1
D
)A.-1
B.-0.729
C.0
D.1
答案:
D 解析:由题知,点$A_{10}$的坐标为(1,0),则$y_{10}=0$.
∵ 函数图像关于点(1,0)中心对称,
∴ $y_{9}+y_{11}=y_{8}+y_{12}=…=y_{1}+y_{19}=0$.将x=2代入函数表达式,y=$2^{3}-3×2^{2}+3×2-1=1$,即$y_{20}=1$.
∴ $y_{1}+y_{2}+y_{3}+…+y_{19}+y_{20}$的值为1.
∵ 函数图像关于点(1,0)中心对称,
∴ $y_{9}+y_{11}=y_{8}+y_{12}=…=y_{1}+y_{19}=0$.将x=2代入函数表达式,y=$2^{3}-3×2^{2}+3×2-1=1$,即$y_{20}=1$.
∴ $y_{1}+y_{2}+y_{3}+…+y_{19}+y_{20}$的值为1.
5. (2024·赤峰)编号为A、B、C、D、E的五台收割机,若同时启动其中两台收割机,收割面积相同的田地所需时间如表,则收割最快的一台收割机编号是____.
|收割机编号|A、B|B、C|C、D|D、E|A、E|
|所需时间/时|23|19|20|22|18|
|收割机编号|A、B|B、C|C、D|D、E|A、E|
|所需时间/时|23|19|20|22|18|
答案:
C 解析:
∵ A、B所需时间为23小时,B、C所需时间为19小时,
∴ C比A快4小时.
∵ B、C所需时间为19小时,C、D所需时间为20小时,
∴ B比D快1小时.
∵ C、D所需时间为20小时,D、E所需时间为22小时,
∴ C比E快2小时.
∵ D、E所需时间为22小时,A、E所需时间为18小时,
∴ A比D快4小时.如图.
∴ C<E<A<B<D.
∴ 收割最快的一台收割机编号是C.

C 解析:
∵ A、B所需时间为23小时,B、C所需时间为19小时,
∴ C比A快4小时.
∵ B、C所需时间为19小时,C、D所需时间为20小时,
∴ B比D快1小时.
∵ C、D所需时间为20小时,D、E所需时间为22小时,
∴ C比E快2小时.
∵ D、E所需时间为22小时,A、E所需时间为18小时,
∴ A比D快4小时.如图.
∴ C<E<A<B<D.
∴ 收割最快的一台收割机编号是C.

查看更多完整答案,请扫码查看


