《2025年通城学典全程测评卷九年级数学全一册苏科版》

12. (19分)(2024·陕西)
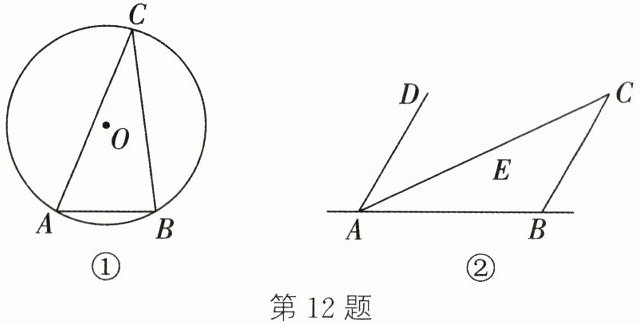
(1) 如图①,在$\triangle ABC$中,$AB= 15$,$\angle C= 30^{\circ }$,作$\triangle ABC的外接圆\odot O$,则$\overset{\frown}{ACB}$的长为____(结果保留$\pi$).
(2) 如图②,道路$AB$的一侧是湿地.某生态研究所在湿地上建有观测点$D、E、C$,线段$AD、AC和BC$为观测步道,其中点$A和点B$为观测步道出入口.已知点$E在AC$上,且$AE= EC$,$\angle DAB= 60^{\circ }$,$\angle ABC= 120^{\circ }$,$AB= 1200\ m$,$AD= BC= 900\ m$,现要在湿地上修建一个新观测点$P$,使$\angle DPC= 60^{\circ }$.再在线段$AB上选一个新的步道出入口点F$,并修建三条新步道$PF、PD、PC$,使新步道$PF经过观测点E$,并将五边形$ABCPD$的面积平分.是否存在满足要求的点$P和点F$? 若存在,求此时$PF$的长;若不存在,请说明理由(点$A、B、C、P、D$在同一平面内,道路$AB$与观测步道的宽、观测点及出入口的大小忽略不计,结果保留根号).

答案：

(1)25π　解析:连接OA、OB,如图①所示.
∵∠C=30°,
∴∠AOB=60°.
∵OA=OB,
∴△OAB是等边三角形.
∵AB=15,
∴OA=OB=15.
∴$\overset{\frown}{ACB}$的长为$\frac{300π×15}{180}$=25π
(2)存在满足要求的点P和点F　连接CD.
∵∠DAB=60°,∠ABC=120°,
∴∠DAB+∠ABC=180°.
∴AD//BC.
∵AD=BC=900m,
∴四边形ABCD是平行四边形.
∵要在湿地上修建一个新观测点P,使∠DPC=60°,
∴点P在以点O为圆心、CD为弦、圆心角为120°的圆上,如图②所示.
∵AE=EC,
∴经过点E的直线都平分四边形ABCD 的面积,
∵新步道PF经过观测点E，并将五边形ABCPD 的面积平分，
∴直线PF必经过CD的中点M.
∴ME是△CAD的中位线.
∴ME//AD.
∵MF//AD,DM//AF,
∴四边形AFMD是平行四边形.
∴FM=AD=900m.作CN⊥PF于点N,如图③所示.
∵四边形AFMD是平行四边形,∠DAB=60°,
∴∠PMC=∠DMF=∠DAB=60°.
∵CM=$\frac{1}{2}$CD=$\frac{1}{2}$AB=600m,
∴MN=CM·cos60°=300m.
∴CN=CM·sin60°=300$\sqrt{3}$m.
∵∠PMC=∠DPC=60°,
∴△PMC∽△DPC.
∴$\frac{PC}{CD}$=$\frac{CM}{PC}$,即$\frac{PC}{1200}$=$\frac{600}{PC}$.
∴PC²=720000m².在Rt△PCN中,PN=$\sqrt{PC^2 - CN^2}$=$\sqrt{720000 - 270000}$=300$\sqrt{5}$(m).
∴PF=300$\sqrt{5}$+300+900=(300$\sqrt{5}$+1200)m.
∴存在满足要求的点P和点F,此时PF的长为(300$\sqrt{5}$+1200)m