《2025年通城学典全程测评卷九年级数学全一册苏科版》

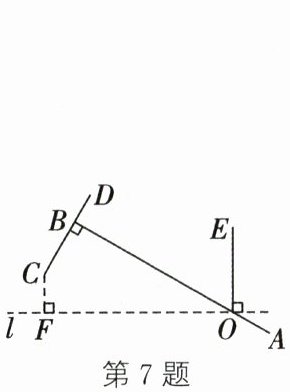
7. 如图,$AB\perp CD于点B$,$AB与水平线l相交于点O$,$OE\perp l$.若$BC= 4$分米,$OB= 12$分米,$\angle BOE= 60^{\circ }$,则点$C到水平线l的距离CF$为____分米(结果用含根号的式子表示).

答案：
(6 - 2$\sqrt{3}$)　解析:如图,延长DC交l于点H,连接OC.在Rt△OBH中,∠BOH=90° - 60°=30°,OB=12分米.
∴BH=12×tan30°=4$\sqrt{3}$(分米),OH=8$\sqrt{3}$分米.
∵S△OBH=S△OCH+S△OBC,
∴$\frac{1}{2}$OB·BH=$\frac{1}{2}$OH·CF+$\frac{1}{2}$OB·BC.
∴$\frac{1}{2}$×12×4$\sqrt{3}$=$\frac{1}{2}$×8$\sqrt{3}$×CF+$\frac{1}{2}$×12×4.
∴CF=(6 - 2$\sqrt{3}$)分米.
　　　　　　　

8. 新趋势 跨学科 (2024·西宁)阅读相关资料:① 如图①,在地球仪上,与赤道平行的圆圈叫做纬线;② 西宁市的纬度约为北纬$37^{\circ }$;③ 如图②,赤道半径$OA$约为6400千米,弦$BC// OA$,以$BC为直径的圆的周长就是北纬37^{\circ }$纬线的长度.根据以上信息,北纬$37^{\circ }$纬线的长度约为____千米(参考数据:$\pi \approx 3,\sin 37^{\circ }\approx 0.6,\cos 37^{\circ }\approx 0.8,\tan 37^{\circ }\approx 0.8$).

答案：
30720　解析:过点O作OD⊥BC于点D,如图所示.
∴易得BD=CD=$\frac{1}{2}$BC.
∵BC//OA,∠AOB=37°,
∴∠CBO=∠AOB=37°.在Rt△OBD中,OB=6400千米,cos∠CBO=$\frac{BD}{OB}$.
∴BD=OB·cos∠CBO=6400×cos37°≈6400×0.8=5120(千米).
∴BC=2BD=2×5120=10240(千米).
∴以BC为直径的圆的周长为BC·π=10240π≈10240×3=30720(千米).
∴北纬37°纬线的长度约为30720千米
　　　　　　　　

9. (2024·深圳)如图,在$\triangle ABC$中,$AB= BC$,$\tan B= \frac {5}{12}$,$D为BC$上一点,若满足$CD= \frac {5}{8}BD$,过点$D作DE\perp AD$,交$AC的延长线于点E$,则$\frac {CE}{AC}= $____.

答案：
$\frac{20}{21}$　解析:如图,过点A作AH⊥CB于点H,作CM⊥AD于点M.
∵AB=BC,CD=$\frac{5}{8}$BD,
∴设BD=8a,则CD=5a.
∴BC=AB=BD+CD=13a.
∵tanB=$\frac{5}{12}$,
∴AH=5a,BH=12a.
∴DH=BH - BD=4a,CH=a.在Rt△ACH中,AC=$\sqrt{AH^2 + CH^2}$=$\sqrt{26}$a;在Rt△ADH 中,AD=$\sqrt{AH^2 + DH^2}$=$\sqrt{41}$a.
∴cos∠ADC=$\frac{DH}{AD}$=$\frac{4\sqrt{41}}{41}$.
∴DM=CD·cos∠ADC=$\frac{20\sqrt{41}}{41}$a.
∴AM=AD - DM=$\frac{21\sqrt{41}}{41}$a.
∵CM⊥AD,DE⊥AD,
∴CM//DE.
∴△AMC∽△ADE.
∴易得$\frac{CE}{AC}$=$\frac{DM}{AM}$=$\frac{20}{21}$.
　　　　　　　　

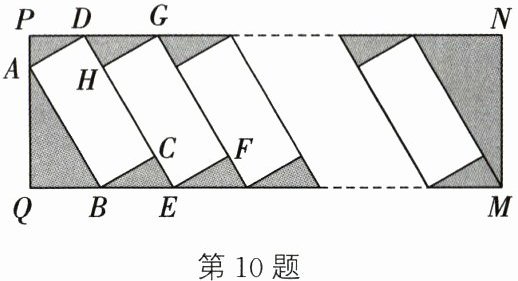
10. (16分)(2024·广东)我国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求,某小区增设了充电站,如图所示为矩形$PQMN$充电站的平面示意图,矩形$ABCD$是其中一个停车位.经测量,$\angle ABQ= 60^{\circ }$,$AB= 5.4\ m$,$CE= 1.6\ m$,$GH\perp CD$,$GH$是另一个停车位的宽,所有停车位的长宽相同,按图示并列划定.根据信息回答问题:(参考数据:$\sqrt {3}\approx 1.73$)
(1) 求$PQ$的长;(结果精确到$0.1\ m$)
(2) 该充电站有20个停车位,求$PN$的长.

答案：
(1)
∵四边形PQMN是矩形
∴∠Q=∠P=90°.在Rt△ABQ中,∠ABQ=60°,AB=5.4m,
∴AQ=AB·sin∠ABQ=$\frac{27\sqrt{3}}{10}$m,∠QAB=30°.
∵四边形ABCD是矩形,
∴AD=BC,∠BAD=∠BCD=∠ABC=∠BCE=90°.
∴∠CBE=30°.
∴BC=$\frac{CE}{\tan∠CBE}$=$\frac{8\sqrt{3}}{5}$m.
∴AD=$\frac{8\sqrt{3}}{5}$m.
∵∠PAD=180° - 30° - 90°=60°,
∴AP=AD·cos∠PAD=$\frac{4\sqrt{3}}{5}$m.
∴PQ=AP+AQ=$\frac{7\sqrt{3}}{2}$≈6.1m
(2)在Rt△BCE中,BE=$\frac{CE}{\sin∠CBE}$=3.2m;在Rt△ABQ 中,BQ=AB·cos∠ABQ=2.7m.
∵该充电站有20个停车位,
∴QM=QB+20BE=66.7m.
∵四边形PQMN是矩形,
∴PN=QM=66.7m

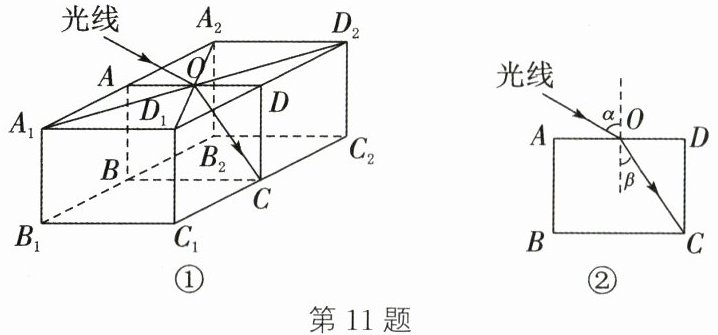
11. (16分)(2024·广元)小明从科普读物中了解到,光从真空射入介质发生折射时,入射角$\alpha的正弦值与折射角\beta的正弦值的比值\frac {\sin \alpha }{\sin \beta }$叫做介质的“绝对折射率”,简称“折射率”,它表示光在介质中传播时,介质对光作用的一种特征.
(1) 若光从真空射入某介质,入射角为$\alpha$,折射角为$\beta$,且$\cos \alpha =\frac {\sqrt {7}}{4}$,$\beta =30^{\circ }$,求该介质的折射率.
(2) 现有一块与(1)中折射率相同的长方体介质,如图①所示,点$A、B、C、D$分别是长方体棱的中点,若光线经真空从矩形$A_{1}D_{1}D_{2}A_{2}对角线交点O$处射入,其折射光线恰好从点$C$处射出.如图②,$\alpha =60^{\circ }$,$CD= 10\ cm$,求截面$ABCD$的面积.

答案：

(1)
∵cosα=$\frac{\sqrt{7}}{4}$,
∴如图,设b=$\sqrt{7}$x,则c=4x.由勾股定理得,a=$\sqrt{(4x)^2 - (\sqrt{7}x)^2}$=3x.
∴sinα=$\frac{a}{c}$=$\frac{3x}{4x}$=$\frac{3}{4}$.又
∵β=30°,
∴sinβ=sin30°=$\frac{1}{2}$.
∴折射率为$\frac{\sinα}{\sinβ}$=$\frac{\frac{3}{4}}{\frac{1}{2}}$=$\frac{3}{2}$　
(2)由题意，可得α=60°,折射率为$\frac{3}{2}$.
∴$\frac{\sinα}{\sinβ}$=$\frac{\sin60°}{\sinβ}$=$\frac{3}{2}$.
∴sinβ=$\frac{\sqrt{3}}{3}$.
∵四边形ABCD是矩形,O是AD的中点,
∴AD=2OD,∠D=90°.又
∵易知∠OCD=β,
∴sin∠OCD=sinβ=$\frac{\sqrt{3}}{3}$.在Rt△ODC中,设OD=$\sqrt{3}$xcm,则OC=3xcm.由勾股定理得,CD=$\sqrt{(3x)^2 - (\sqrt{3}x)^2}$=$\sqrt{6}$xcm.
∴tanβ=$\frac{OD}{CD}$=$\frac{\sqrt{2}}{2}$.
∴OD=10×$\frac{\sqrt{2}}{2}$=5$\sqrt{2}$(cm).
∴AD=2OD=10$\sqrt{2}$(cm).
∴截面ABCD的面积为AD×CD=10$\sqrt{2}$×10=100$\sqrt{2}$(cm²)