《2025年通城学典全程测评卷九年级数学全一册苏科版》

11. (20分)(2024·宿迁)在综合实践活动课上,同学们以折叠正方形纸片展开数学探究活动.
【操作判断】
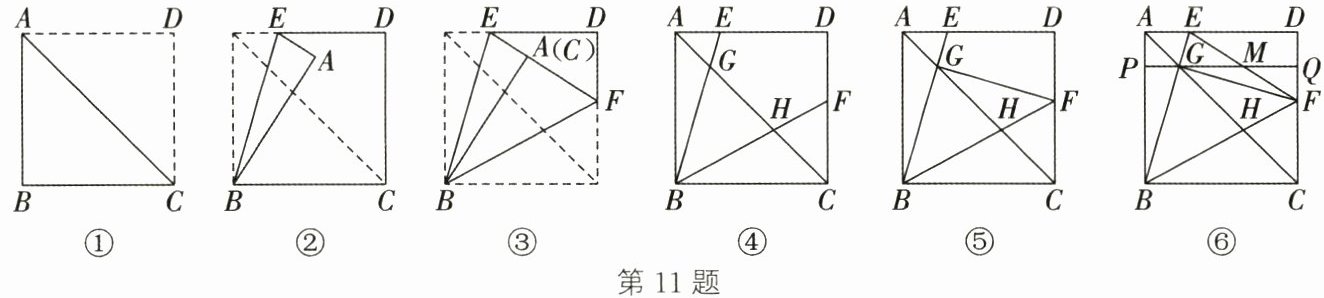
操作一:如图①,对折正方形纸片$ABCD$,得到折痕$AC$,把纸片展平;
操作二:如图②,在边$AD上选一点E$,沿$BE$折叠,使点$A$落在正方形内部,得到折痕$BE$;
操作三:如图③,在边$CD上选一点F$,沿$BF$折叠,使边$BC与边BA$重合,得到折痕$BF$,把正方形纸片展平,得到图④,折痕$BE$、$BF与AC的交点分别为G$、$H$.
根据以上操作,得$\angle EBF= $____$^{\circ}$.
【探究证明】
(1) 如图⑤,连接$GF$,试判断$\triangle BFG$的形状并证明.
(2) 如图⑥,连接$EF$,过点$G作CD$的垂线,分别交$AB$、$CD$、$EF于点P$、$Q$、$M$.求证:$EM= MF$.
【深入研究】
(3) 若$\frac{AG}{AC}= \frac{1}{k}$,请求出$\frac{GH}{HC}$的值(用含$k$的代数式表示).

答案：
【操作判断】45 解析:如图①,由题意,可得∠1=∠2,∠3=∠4.
∵2∠2+2∠3=90°,
∴∠2+∠3=45°.
∴∠EBF=45°.
【探究证明】
(1)△BFG为等腰直角三角形 由题意可得∠EBF=45°.
∵四边形ABCD是正方形,
∴∠BCA=∠ACD=45°.
∴∠EBF=∠ACD.又
∵∠BHA=∠CHF,
∴△BHG∽△CHF.
∴$\frac{BH}{CH}$=$\frac{HG}{HF}$,
∴$\frac{BH}{HG}$=$\frac{CH}{HF}$.
∵∠GHF=∠BHC,
∴△GHF∽△BHC.
∴∠BCH=∠GFH=45°.
∴∠BGF=90°.
∴△BGF为等腰直角三角形.
(2)
∵△GBF为等腰直角三角形,
∴∠BGF=90°,BG=FG.
∴易得∠PBG=∠QGF.
∵PQ⊥AB,PQ⊥CD,
∴∠BPG=∠GQF=90°.
∴△PBG≌△QGF.
∴∠PGB=∠GFQ.
∵PQ//AD,
∴∠PGB=∠AEB.
∵折叠,
∴∠AEB=∠BEF.
∵∠PGB=∠EGQ,
∴∠BEF=∠EGQ.
∵∠BEF+∠EFG=∠EGQ+∠FGQ=90°,
∴∠EFG=∠FGQ.
∴EM=MG=MF. 【深入研究】
(3)如图②,延长BF交PQ的延长线于点N,则$\frac{GH}{CH}$=$\frac{GN}{BC}$.由
(2)知,M为EF的中点,且PQ//AD,
∴Q为DF的中点,即DQ=QF=AP.设DQ=a.
∴CF=CD - DF=ak - 2a.
∴$\frac{QN}{BC}$=$\frac{QF}{FC}$,即$\frac{QN}{ka}$=$\frac{a}{(k - 2)a}$,
∴QN=$\frac{ka}{k - 2}$.
∵QG=PQ - PG=ak - a,
∴GN=QG+QN=$\frac{a(k^2 - 2k +，2)}{k - 2}$.
∴$\frac{GH}{CH}$=$\frac{GN}{BC}$=$\frac{k^2 - 2k + 2}{k^2 - 2k}$.