第112页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
1. 如图,在$□ ABCD$中,$E$、$F分别是边BC$、$CD$的中点,$AE$、$AF分别交BD于点G$、$H$,则图中涂色部分的面积之和与$□ ABCD$的面积之比为 (
A.$7:12$
B.$7:24$
C.$13:36$
D.$13:72$
B
)A.$7:12$
B.$7:24$
C.$13:36$
D.$13:72$
答案:
B 解析:
∵BE//AD,E是BC的中点,
∴△BEG∽△DAG.
∴$\frac{BG}{DG}$=$\frac{BE}{DA}$=$\frac{1}{2}$,即BG=$\frac{1}{3}$BD.同理可得,DH=$\frac{1}{3}$BD.
∴GH=$\frac{1}{3}$BD.
∴$S_{\triangle AGH}$=$\frac{1}{3}$$S_{\triangle ABD}$=$\frac{1}{6}$$S_{□ABCD}$.
∵E、F分别是边BC、CD的中点,
∴EF是△BCD的中位线.
∴EF//BD,EF=$\frac{1}{2}$BD.
∴△CEF∽△CBD.
∴$\frac{S_{\triangle CEF}}{S_{\triangle CBD}}$=($\frac{1}{2}$)²=$\frac{1}{4}$.
∴$S_{\triangle CEF}$=$\frac{1}{4}$$S_{\triangle BCD}$=$\frac{1}{8}$$S_{□ABCD}$.
∴图中涂色部分的面积之和=($\frac{1}{6}$+$\frac{1}{8}$)$S_{□ABCD}$=$\frac{7}{24}$$S_{□ABCD}$,即图中涂色部分的面积之和与$S_{□ABCD}$的面积之比为7:24.
∵BE//AD,E是BC的中点,
∴△BEG∽△DAG.
∴$\frac{BG}{DG}$=$\frac{BE}{DA}$=$\frac{1}{2}$,即BG=$\frac{1}{3}$BD.同理可得,DH=$\frac{1}{3}$BD.
∴GH=$\frac{1}{3}$BD.
∴$S_{\triangle AGH}$=$\frac{1}{3}$$S_{\triangle ABD}$=$\frac{1}{6}$$S_{□ABCD}$.
∵E、F分别是边BC、CD的中点,
∴EF是△BCD的中位线.
∴EF//BD,EF=$\frac{1}{2}$BD.
∴△CEF∽△CBD.
∴$\frac{S_{\triangle CEF}}{S_{\triangle CBD}}$=($\frac{1}{2}$)²=$\frac{1}{4}$.
∴$S_{\triangle CEF}$=$\frac{1}{4}$$S_{\triangle BCD}$=$\frac{1}{8}$$S_{□ABCD}$.
∴图中涂色部分的面积之和=($\frac{1}{6}$+$\frac{1}{8}$)$S_{□ABCD}$=$\frac{7}{24}$$S_{□ABCD}$,即图中涂色部分的面积之和与$S_{□ABCD}$的面积之比为7:24.
2. 如图,在$\triangle ABC$中,$D为BC$上一点,$E为AC$上一点,$AD$、$BE交于点G$,且$AG:GD= 4:1$,$BD:DC= 2:3$,则$AE:EC$的值是 ( )
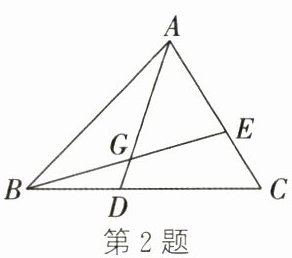
A.$\frac{3}{2}$
B.$\frac{4}{3}$
C.$\frac{6}{5}$
D.$\frac{8}{5}$

A.$\frac{3}{2}$
B.$\frac{4}{3}$
C.$\frac{6}{5}$
D.$\frac{8}{5}$
答案:
D 解析:如图,作AF//BC交BE的延长线于点F.
∴$\frac{AF}{BD}$=$\frac{AG}{GD}$=$\frac{4}{1}$,$\frac{AE}{CE}$=$\frac{AF}{BC}$.
∴AF=4BD.
∵BD:DC=2:3,
∴BD:BC=2:5.
∴BC=$\frac{5}{2}$BD.
∴$\frac{AE}{CE}$=$\frac{AF}{BC}$=$\frac{4BD}{\frac{5}{2}BD}$=$\frac{8}{5}$.

D 解析:如图,作AF//BC交BE的延长线于点F.
∴$\frac{AF}{BD}$=$\frac{AG}{GD}$=$\frac{4}{1}$,$\frac{AE}{CE}$=$\frac{AF}{BC}$.
∴AF=4BD.
∵BD:DC=2:3,
∴BD:BC=2:5.
∴BC=$\frac{5}{2}$BD.
∴$\frac{AE}{CE}$=$\frac{AF}{BC}$=$\frac{4BD}{\frac{5}{2}BD}$=$\frac{8}{5}$.

3. 如图,在正方形$ABCD$中,$\triangle BPC$是等边三角形,$BP$、$CP的延长线分别交AD于点E$、$F$,连接$BD$、$DP$,$BD与CF相交于点H$,给出下列结论:①$BE= 2AE$;②$\triangle DFP\backsim \triangle BPH$;③$\triangle PFD\backsim \triangle PDB$;④$DP^{2}= PH\cdot PC$.其中正确的个数是 (
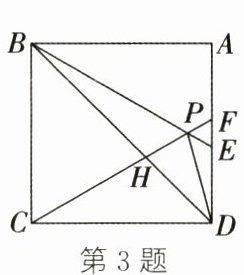
A.$1$
B.$2$
C.$3$
D.$4$
C
)
A.$1$
B.$2$
C.$3$
D.$4$
答案:
C 解析:
∵四边形ABCD是正方形,
∴BC=CD,∠A=∠CBA=90°.
∵△BCP是等边三角形,
∴PC=BC,∠PBC=∠PCB=∠BPC=60°.
∴CD=CP,∠ABE=∠PCD=30°.
∴BE=2AE.故①正确.
∵AD//BC,
∴∠DFP=∠BCP=∠BPH=60°.
∴∠PHB=∠PCB+∠CBH=60°+45°=105°.又
∵CD=CP,∠PCD=30°,
∴∠CPD=∠CDP=75°.
∴∠DPF=105°.
∴∠PHB=∠DPF.
∴△DFP∽△BPH.故②正确.
∵∠DPB=60°+75°=135°≠∠DPF,
∴△PFD与△PDB不相似.故③错误.
∵∠PDH=∠PDC - ∠CDH=75° - 45°=30°,
∴∠PDH=∠PCD.
∵∠DPH=∠CPD,
∴△PDH∽△PCD.
∴$\frac{PD}{PC}$=$\frac{PH}{PD}$.
∴$PD^2$=PH·PC.故④正确.
∵四边形ABCD是正方形,
∴BC=CD,∠A=∠CBA=90°.
∵△BCP是等边三角形,
∴PC=BC,∠PBC=∠PCB=∠BPC=60°.
∴CD=CP,∠ABE=∠PCD=30°.
∴BE=2AE.故①正确.
∵AD//BC,
∴∠DFP=∠BCP=∠BPH=60°.
∴∠PHB=∠PCB+∠CBH=60°+45°=105°.又
∵CD=CP,∠PCD=30°,
∴∠CPD=∠CDP=75°.
∴∠DPF=105°.
∴∠PHB=∠DPF.
∴△DFP∽△BPH.故②正确.
∵∠DPB=60°+75°=135°≠∠DPF,
∴△PFD与△PDB不相似.故③错误.
∵∠PDH=∠PDC - ∠CDH=75° - 45°=30°,
∴∠PDH=∠PCD.
∵∠DPH=∠CPD,
∴△PDH∽△PCD.
∴$\frac{PD}{PC}$=$\frac{PH}{PD}$.
∴$PD^2$=PH·PC.故④正确.
4. (2024·江阴段考)如图,$\triangle ABC$在第一象限,其周长为$16$,点$P从点B$出发,沿$\triangle ABC$的边按“$B-C-A-B$”的路径运动一周,在点$P$运动的同时,作点$P关于原点O的对称点Q$,以$PQ为边作等边三角形PQM$,点$M$在第二象限,则点$M随点P$运动所形成的图形的周长为 (
A.$32$
B.$24$
C.$16\sqrt{3}$
D.$24\sqrt{2}$
C
)A.$32$
B.$24$
C.$16\sqrt{3}$
D.$24\sqrt{2}$
答案:
C 解析:
∵点P从点B出发,沿△ABC的边按“B - C - A - B”的路径运动一周,且点Q关于原点O与点P对称,
∴点Q随点P运动所形成的图形是△ABC关于点O的中心对称图形.设以PQ为边作等边三角形PQM,点M对应A、B、C三点的点分别为$M_a$、$M_b$、$M_c$.
∵△$M_b$$Q_b$B是等边三角形,
∴$M_b$O=$\sqrt{3}$OB.同理,$M_c$O=$\sqrt{3}$OC.
∴$\frac{M_bO}{BO}$=$\frac{M_cO}{CO}$=$\sqrt{3}$.
∵∠COB+∠BOMb=90°,∠$M_c$$OM_b$+∠BOMb=90°,
∴∠COB=∠$M_c$$OM_b$.
∴△$M_c$$OM_b$∽△COB.
∴$M_b$$M_c$=$\sqrt{3}$BC.同理,$M_a$$M_b$=$\sqrt{3}$AB,$M_a$$M_c$=$\sqrt{3}$AC.
∴△$M_a$$M_b$$M_c$的周长=$\sqrt{3}$(AB+BC+CD)=$\sqrt{3}$×16=16$\sqrt{3}$.
∵点P从点B出发,沿△ABC的边按“B - C - A - B”的路径运动一周,且点Q关于原点O与点P对称,
∴点Q随点P运动所形成的图形是△ABC关于点O的中心对称图形.设以PQ为边作等边三角形PQM,点M对应A、B、C三点的点分别为$M_a$、$M_b$、$M_c$.
∵△$M_b$$Q_b$B是等边三角形,
∴$M_b$O=$\sqrt{3}$OB.同理,$M_c$O=$\sqrt{3}$OC.
∴$\frac{M_bO}{BO}$=$\frac{M_cO}{CO}$=$\sqrt{3}$.
∵∠COB+∠BOMb=90°,∠$M_c$$OM_b$+∠BOMb=90°,
∴∠COB=∠$M_c$$OM_b$.
∴△$M_c$$OM_b$∽△COB.
∴$M_b$$M_c$=$\sqrt{3}$BC.同理,$M_a$$M_b$=$\sqrt{3}$AB,$M_a$$M_c$=$\sqrt{3}$AC.
∴△$M_a$$M_b$$M_c$的周长=$\sqrt{3}$(AB+BC+CD)=$\sqrt{3}$×16=16$\sqrt{3}$.
5. (2024·扬州期末)在如图所示的网格中,每个小正方形的边长均为$1$,若$\triangle ABC\backsim \triangle FCE$,则$\triangle FCE$的面积是____
$\frac{16}{3}$
.
答案:
$\frac{16}{3}$ 解析:
∵△ABC∽△FCE,
∴$\frac{S_{\triangle ABC}}{S_{\triangle FCE}}$=($\frac{BC}{CE}$)²=($\frac{3}{4}$)².
∵$S_{\triangle ABC}$=$\frac{1}{2}$×3×2=3,
∴$S_{\triangle FCE}$=$\frac{16}{3}$.
∵△ABC∽△FCE,
∴$\frac{S_{\triangle ABC}}{S_{\triangle FCE}}$=($\frac{BC}{CE}$)²=($\frac{3}{4}$)².
∵$S_{\triangle ABC}$=$\frac{1}{2}$×3×2=3,
∴$S_{\triangle FCE}$=$\frac{16}{3}$.
6. (2024·东台期末)如图,在$\triangle ABC$中,$\angle C= 90^{\circ}$,$AC= 6$,$BC= 8$,$CD是斜边AB$上的中线,点$G是\triangle ABC$的重心,$GH\perp AB于点H$,则$GH= $____.
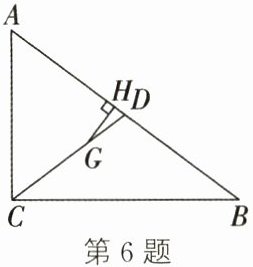

答案:
$\frac{8}{5}$ 解析:过点C作CE⊥AB于点E,如图所示.
∵∠C=90°,AC=6,BC=8,
∴AB=$\sqrt{AC^2 + BC^2}$=10.
∵$\frac{1}{2}$CE·AB=$\frac{1}{2}$AC·BC,
∴CE=$\frac{6×8}{10}$=$\frac{24}{5}$.
∵点G是△ABC的重心,
∴DG=$\frac{1}{2}$CG.
∴DG=$\frac{1}{3}$CD.
∵CE⊥AB,GH⊥AB,
∴GH//CE.
∴△DHG∽△DEC.
∴$\frac{GH}{CE}$=$\frac{DG}{DC}$=$\frac{1}{3}$.
∴GH=$\frac{1}{3}$CE=$\frac{1}{3}$×$\frac{24}{5}$=$\frac{8}{5}$.

$\frac{8}{5}$ 解析:过点C作CE⊥AB于点E,如图所示.
∵∠C=90°,AC=6,BC=8,
∴AB=$\sqrt{AC^2 + BC^2}$=10.
∵$\frac{1}{2}$CE·AB=$\frac{1}{2}$AC·BC,
∴CE=$\frac{6×8}{10}$=$\frac{24}{5}$.
∵点G是△ABC的重心,
∴DG=$\frac{1}{2}$CG.
∴DG=$\frac{1}{3}$CD.
∵CE⊥AB,GH⊥AB,
∴GH//CE.
∴△DHG∽△DEC.
∴$\frac{GH}{CE}$=$\frac{DG}{DC}$=$\frac{1}{3}$.
∴GH=$\frac{1}{3}$CE=$\frac{1}{3}$×$\frac{24}{5}$=$\frac{8}{5}$.

查看更多完整答案,请扫码查看


