《2025年通城学典全程测评卷九年级数学全一册苏科版》

7. 已知$M(a,b)$是平面直角坐标系中的点,其中a是从1、2、3、4这四个数中任取的一个数,b是从1、2、3、4、5这五个数中任取的一个数.定义“点$M(a,b)在直线x+y= n$上”为事件$Q_{n}(2≤n≤9$,n为整数),则当$Q_{n}$的概率最大时,n的所有可能的值为____5或6.

答案： 7.5或6 解析:列表如下:
1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
5 6 7 8 9
∵$a$是从1、2、3、4这四个数中任取的一个数，$b$是从1、2、3、4、5这五个数中任取的一个数，点$M(a,b)$在直线$x + y = n$（$2\leqslant n\leqslant9$，$n$为整数）上，
∴$n = 2$的概率是$\frac{1}{20}$，$n = 3$的概率是$\frac{1}{10}$，$n = 4$的概率是$\frac{3}{20}$，$n = 5$的概率是$\frac{1}{5}$，$n = 6$的概率是$\frac{1}{5}$，$n = 7$的概率是$\frac{3}{20}$，$n = 8$的概率是$\frac{1}{10}$，$n = 9$的概率是$\frac{1}{20}$。
∴当$Q_{n}$的概率最大时，$n = 5$或6。

8. 如果任意选择一对有序整数$(m,n)$,其中$|m|≤1,|n|≤2$,每一对这样的有序整数被选择的可能性是相等的,那么关于x的方程$x^{2}+nx+m= 0$有两个相等实数根的概率是$\frac{1}{5}$.

答案： 8.$\frac{1}{5}$ 解析:
∵$|m|\leqslant1$，$|n|\leqslant2$，
∴$m = 0$、$\pm1$，$n = 0$、$\pm1$、$\pm2$，
∴有序整数$(m,n)$共有15种。
∵方程$x^{2}+nx + m = 0$有两个相等实数根，
∴$b^{2}-4ac=n^{2}-4m = 0$，有$(0,0)$、$(1,2)$、$(1,-2)$三种可能，
∴关于$x$的方程$x^{2}+nx + m = 0$有两个相等实数根的概率是$\frac{3}{15}=\frac{1}{5}$。

9. 从3、0、-1、-2、-3这五个数中随机抽取一个数,作为函数$y= (5-m^{2})x$和关于x的方程$(m+1)\cdot x^{2}+mx+1= 0$中m的值,恰好使所得函数的图像经过第一、三象限,且方程有实数根的概率为$\frac{2}{5}$.

答案： 9.$\frac{2}{5}$ 解析:
∵所得函数的图像经过第一、三象限，
∴$5 - m^{2}＞0$，
∴$m^{2}＜5$，
∴在3、0、$-1$、$-2$、$-3$中，3和$-3$不符合题意。将$m = 0$代入$(m + 1)x^{2}+mx + 1 = 0$，得$x^{2}+1 = 0$，$b^{2}-4ac=-4＜0$，方程无实数根；将$m = -1$代入$(m + 1)x^{2}+mx + 1 = 0$，得$-x + 1 = 0$，解得$x = 1$，方程有实数根；将$m = -2$代入$(m + 1)x^{2}+mx + 1 = 0$，得$x^{2}+2x - 1 = 0$，$b^{2}-4ac=4 + 4 = 8＞0$，方程有实数根，
∴方程有实数根的概率为$\frac{2}{5}$。

10. (2025·南京建邺一模)如图①,一只圆形平盘被同心圆划成M、N、S三个区域,随机向平盘中撒一把豆子,计算落在M、N、S三个区域的豆子数的比,多次重复这个试验,发现落入三个区域的豆子数的比显示出一定的稳定性,总在三个区域的面积之比附近摆动.如图②,将一根筷子放在该盘中AB位置,发现三个圆弧刚好将AB五等分,我们把豆子落入三个区域的概率分别记作$P(M)$、$P(N)$、$P(S)$.已知$P(S)= \frac {1}{5}$,则$P(M)$的值为____.

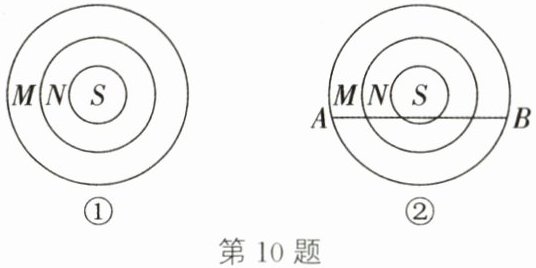
答案：
10.$\frac{8}{15}$ 解析:如图，设$AE=EC=CD=DF=BF=2x$。过点O作$OH\perp CD$于点H，连接OC、OE、OA，则易得$CH=DH=x$。
∵$P(S)=\frac{1}{5}$，
∴$\frac{\pi\cdot OC^{2}}{\pi\cdot OA^{2}}=\frac{1}{5}$，解得$OA=\sqrt{5}OC$。在$Rt\triangle OAH$中，$OH^{2}=OA^{2}-AH^{2}=(\sqrt{5}OC)^{2}-(5x)^{2}=5OC^{2}-25x^{2}$；在$Rt\triangle OCH$中，$OH^{2}=OC^{2}-CH^{2}=OC^{2}-x^{2}$，
∴$5OC^{2}-25x^{2}=OC^{2}-x^{2}$，解得$OC=\sqrt{6}x$，
∴$OH^{2}=5x^{2}$，$OA=\sqrt{30}x$。在$Rt\triangle OEH$中，$OE^{2}=OH^{2}+EH^{2}=5x^{2}+9x^{2}=14x^{2}$，
∴$P(M)=\frac{\pi\cdot OA^{2}-\pi\cdot OE^{2}}{\pi\cdot OA^{2}}=\frac{\pi\cdot30x^{2}-\pi\cdot14x^{2}}{\pi\cdot30x^{2}}=\frac{8}{15}$。

11. (15分)(2024·长春)2021年吉林省普通高中开始施行新高考选科模式,此模式有若干种学科组合,每名高中生可根据自己的实际情况选择一种.一对双胞胎姐妹考入同一所高中且选择了相同组合,该校要将所有选报这种组合的学生分成A、B、C三个班,其中每名学生被分到这三个班的机会均等.用画树状图或列表的方法,求这对双胞胎姐妹被分到同一个班的概率.

答案： 11.列表如下:
A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
共有9种等可能的结果，其中这对双胞胎姐妹被分到同一个班的结果有(A,A)、(B,B)、(C,C)，共3种，
∴这对双胞胎姐妹被分到同一个班的概率为$\frac{3}{9}=\frac{1}{3}$。

12. (15分)生物科学家通过大量的调查估计得出,某种树木生长高10m以上的概率为0.9,生长高15m以上的概率为0.4,生长高18m以上的概率为0.1,现高10m的这种树长到15m的概率为多少?现高15m的这种树长到18m的概率为多少?

答案： 12.设所有被调查的总棵数为$n$，其中长到10m、15m和18m的这种树的棵数分别为$m_{1}$、$m_{2}$、$m_{3}$。由题意，有$\frac{m_{1}}{n}=0.9$，$\frac{m_{2}}{n}=0.4$，$\frac{m_{3}}{n}=0.1$，即$m_{1}=0.9n$，$m_{2}=0.4n$，$m_{3}=0.1n$，
∴现高10m的这种树长到15m的概率为$\frac{m_{2}}{m_{1}}=\frac{0.4n}{0.9n}=\frac{4}{9}$；现高15m的这种树长到18m的概率为$\frac{m_{3}}{m_{2}}=\frac{0.1n}{0.4n}=\frac{1}{4}$。