《2025年通城学典全程测评卷九年级数学全一册苏科版》

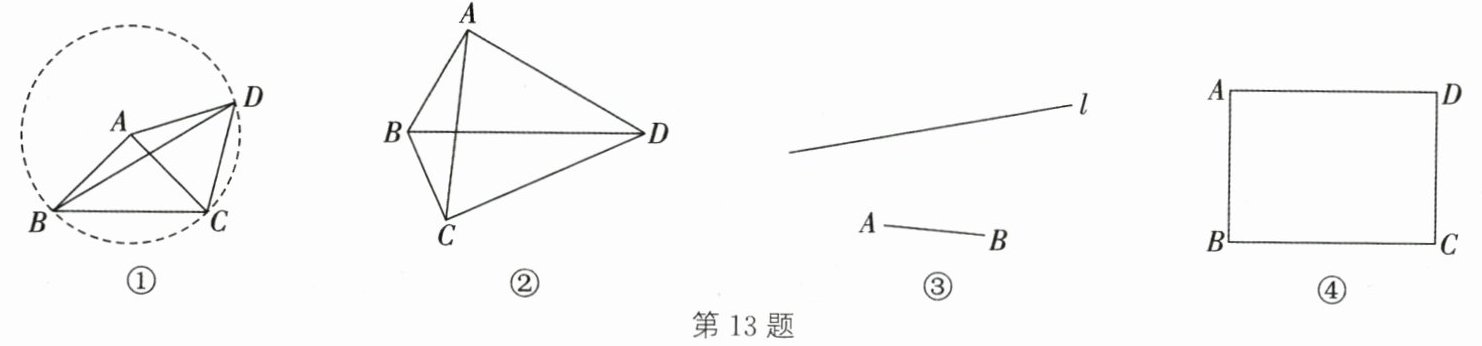
13. (20分)(2024·连云港灌云期中)【学习心得】
(1) 小雯同学在学习完“圆”这一章内容后,感觉到一些几何问题如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.
例如:如图①,在$△ABC$中,$AB= AC,∠BAC= 90^{\circ }$,D是$△ABC$外一点,且$AD= AC$,求$∠BDC$的度数.若以点A为圆心,AB长为半径作辅助圆$\odot A$,则C、D两点必在$\odot A$上,$∠BAC是\odot A$的圆心角,$∠BDC是\odot A$的圆周角,则$∠BDC= $____$^{\circ }$.
【初步运用】
(2) 如图②,在四边形ABCD中,$∠BAD= ∠BCD= 90^{\circ },∠BDC= 24^{\circ }$,求$∠BAC$的度数.
【方法迁移】
(3) 如图③,有线段AB和直线l,用直尺和圆规在l上作出所有的点P,使得$∠APB= 30^{\circ }$(不写作法,保留作图痕迹).
【问题拓展】
(4) 如图④,在矩形ABCD中,$AB= 2,BC= m$,M为线段CD上的点.若满足$∠AMB= 45^{\circ }$的点M恰好有两个,则m的取值范围为____.

答案：

(1) 45 解析:
∵AB=AC=AD,
∴B、C、D三点都在以点A为圆心、以AB长为半径的圆上.
∵∠BAC=90°,
∴∠BDC=1/2∠BAC=45°.
(2) 如图①,取BD的中点E,连接AE、CE.
∵∠BAD=∠BCD=90°,E为BD的中点,
∴AE=BE=DE=CE=1/2BD.
∴A、B、C、D四点在以点E为圆心、1/2BD长为半径的圆上.
∴∠BAC=∠BDC=24°.
(3) 如图②,点P₁、P₂即为所求.
(4) 2≤m＜√2+1 解析:如图③,在BC上截取一点F,使得BF=BA,连接AF,以AF为直径作⊙O,过点F作EF⊥AD,交AD于点E,过点O作OG⊥EF,交EF于点H,交⊙O于点G,过点G作⊙O的切线,分别交AD、BC于点K、Q,则四边形ABFE为正方形.
∵四边形ABCD是矩形,
∴∠ABF=90°.
∴点B在⊙O上,AF=√(AB²+BF²)=2√2.
∴OG=OF=√2.
∵OH⊥EF,
∴FH=1/2EF=1/2AB=1.
∴OH=√(OF² - FH²)=1.
∴GH=OG - OH=√2 - 1.
∴BF≤m＜BQ.
∴2≤m＜2+√2 - 1,即2≤m＜√2+1.