《2025年通城学典全程测评卷六年级数学上册苏教版江苏专版》

3. 新情境 生活应用 妈妈给爷爷、奶奶准备了一个水果礼品盒,这个礼品盒长30厘米,宽25厘米,高14厘米。如果用丝带把礼品盒捆扎起来,打结处要用45厘米长的丝带(如图),那么一共需要多少厘米长的丝带？(4分)

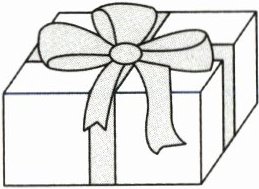
答案： 30×2=60(厘米) 25×2=50(厘米) 14×4=56(厘米) 60+50+56+45=211(厘米)

4. 新素养 创新意识 为了调查一个“跑冒滴漏”水龙头的漏水情况,颖颖设计了一个实验。
第一步：第一天晚上10:00,取一个长12厘米、宽10厘米、高15厘米的空长方体容器,先倒入一些水,使水面高度为2厘米,接着放在水龙头下面接水。
第二步：测量出这个水龙头每分钟滴水40滴。
第三步：到第二天早上7:00,测量出这个容器的水面高度为11厘米。
你能根据以上信息计算出每滴水多少毫升吗？(4分)

答案： 12×10×(11 - 2)=1080(立方厘米) 1080立方厘米=1080毫升 7+12 - 10=9(时) 9×60×40=21600(滴) 1080÷21600=0.05(毫升)

5. 用混凝土浇筑一个无盖的长方体水槽(如图),从外面量,长12dm,宽8dm,高6dm,混凝土厚1dm。

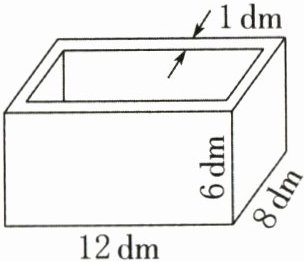
(1)这个水槽的占地面积是多少平方分米？(4分)
(2)最多可盛水多少升？(4分)
(3)浇筑这样一个水槽需要混凝土多少立方分米？(4分)

答案：
(1)12×8=96(dm²)
(2)12 - 1×2=10(dm) 8 - 1×2=6(dm) 6 - 1=5(dm) 10×6×5=300(dm³) 300dm³=300L 解析:求长方体水槽的容积时,长度要从里面量,长、宽分别要用从外面量的长度减去两个混凝土的厚度,根据题意,这个水槽是无盖的,所以从里面量的高只要用从外面量的高减去下面的一个混凝土的厚度即可。
(3)12×8×6=576(dm³) 576 - 300=276(dm³)

附加题。(10分)
有一个长方体,若长增加2厘米,则体积增加24立方厘米；若宽增加3厘米,则体积增加45立方厘米；若高增加4厘米,则体积增加80立方厘米。原来长方体的表面积是多少平方厘米？

答案： (24÷2+45÷3+80÷4)×2=94(平方厘米) 解析:根据"若长增加2厘米,则体积增加24立方厘米",得出原来长方体的左(右)面的面积=24÷2=12(平方厘米);同理,原来长方体的前(后)面的面积=45÷3=15(平方厘米),原来长方体的上(下)面的面积=80÷4=20(平方厘米),进而求出原来长方体的表面积。