第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
四、手工作坊。(共 8 分)
在下面的方格纸中,每个小方格的面积表示 1 平方厘米。
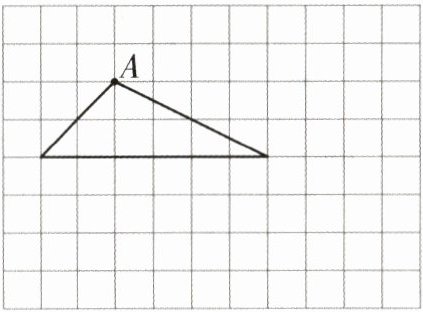
1. 以 A 为端点画一条线段,将这个三角形分成面积相等的两个小三角形。(4 分)
2. 在方格纸中画一个平行四边形,使它的高和面积与已知三角形的高和面积分别相等。(4 分)
在下面的方格纸中,每个小方格的面积表示 1 平方厘米。

1. 以 A 为端点画一条线段,将这个三角形分成面积相等的两个小三角形。(4 分)
2. 在方格纸中画一个平行四边形,使它的高和面积与已知三角形的高和面积分别相等。(4 分)
答案:
1. 如图 2. 画法不唯一,如图
1. 如图 2. 画法不唯一,如图

1. 新情境 人文历史 我国是最早发现并利用茶的国家,六安瓜片更是有悠久的历史,据《六安州志》记载:“茶之极品,明朝始入贡。”说明六安瓜片在明朝就已经很出名了。现有一块底为 2 千米、高为 600 米的三角形茶园,这块茶园的面积为多少公顷? 若每公顷产茶叶 1600 千克,则这块茶园可产茶叶多少吨?(8 分)
答案:
2千米=2000米 2000×600÷2=600000(平方米) 600000平方米=60公顷 1600×60=96000(千克) 96000千克=96吨
2. 新情境 生活应用 锡箔纸可以用来烘烤食物。如图,李阿姨将一张长方形锡箔纸折叠成一个梯形。(单位:分米)

(1)梯形的高等于(
A. 长方形的长
B. 长方形的宽
C. 长方形的周长
D. 长方形的面积
(2)在梯形锡箔纸上摆放鸡翅(只放一层),每个鸡翅占 40 平方厘米,最多能摆放多少个鸡翅?(6 分)

(1)梯形的高等于(
B
),梯形的下底等于(A
)。(6 分)A. 长方形的长
B. 长方形的宽
C. 长方形的周长
D. 长方形的面积
(2)在梯形锡箔纸上摆放鸡翅(只放一层),每个鸡翅占 40 平方厘米,最多能摆放多少个鸡翅?(6 分)
(7+7+3+3)×4÷2=40(平方分米) 40平方分米=4000平方厘米 4000÷40=100(个)
答案:
(1)B A (2)(7+7+3+3)×4÷2=40(平方分米) 40平方分米=4000平方厘米 4000÷40=100(个)
3. 新趋势 操作探究 在学习了梯形面积之后,同学们又进行了深入的研究,如下图。(每个小方格的边长表示 1 厘米)
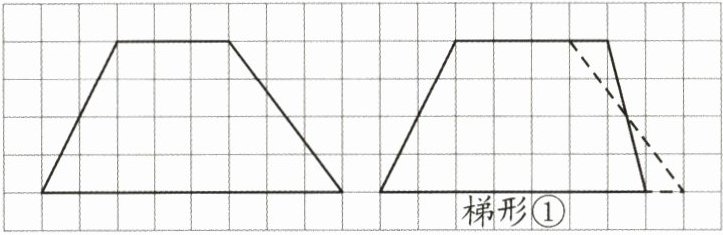
(1)小明在图中将这个梯形的上底增加 1 厘米,下底减少 1 厘米,高不变,得到新的梯形①,发现梯形①的面积与原梯形的面积相等,都是(
(2)小明提出了一个猜想:在梯形的高不变的情况下,上底增加几厘米,下底减少相同的几厘米(减少的厘米数小于下底),则面积不变。你同意他的猜想吗? 请你举一个例子验证下吧。(6 分)
(3)除了举例验证外,你还可以用什么方法来验证? 写出你的思考过程。(6 分)

(1)小明在图中将这个梯形的上底增加 1 厘米,下底减少 1 厘米,高不变,得到新的梯形①,发现梯形①的面积与原梯形的面积相等,都是(
22
)平方厘米。(4 分)(2)小明提出了一个猜想:在梯形的高不变的情况下,上底增加几厘米,下底减少相同的几厘米(减少的厘米数小于下底),则面积不变。你同意他的猜想吗? 请你举一个例子验证下吧。(6 分)
同意 举例不唯一,如一个梯形的上底是3厘米,下底是9厘米,高是5厘米,上底增加2厘米,下底减少2厘米,高不变。原来梯形的面积:(3+9)×5÷2=30(平方厘米),现在梯形的面积:[(3+2)+(9-2)]×5÷2=30(平方厘米),30=30,面积不变
(3)除了举例验证外,你还可以用什么方法来验证? 写出你的思考过程。(6 分)
方法不唯一,如梯形的面积公式为S=(a+b)×h÷2,上底增加1,同时下底减少1,此时梯形的面积S=(a+1+b-1)×h÷2=(a+b)×h÷2,面积不变
答案:
(1)22 (2)同意 举例不唯一,如一个梯形的上底是3厘米,下底是9厘米,高是5厘米,上底增加2厘米,下底减少2厘米,高不变。原来梯形的面积:(3+9)×5÷2=30(平方厘米),现在梯形的面积:[(3+2)+(9-2)]×5÷2=30(平方厘米),30=30,面积不变 (3)方法不唯一,如梯形的面积公式为S=(a+b)×h÷2,上底增加1,同时下底减少1,此时梯形的面积S=(a+1+b-1)×h÷2=(a+b)×h÷2,面积不变
查看更多完整答案,请扫码查看


