第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
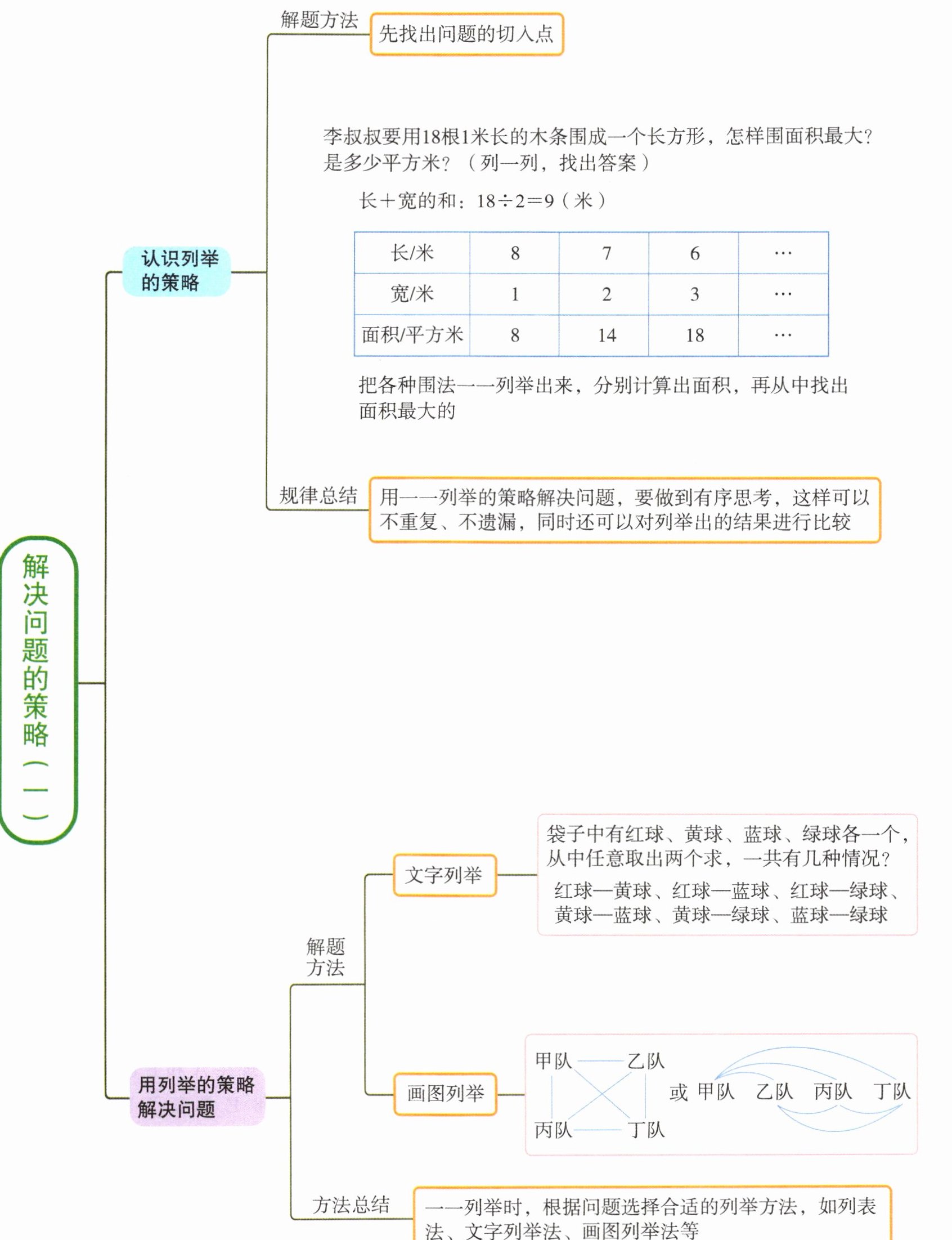
解题方法 先找出问题的切入点
李叔叔要用18根1米长的木条围成一个长方形,怎样围面积最大?是多少平方米?(列一列,找出答案)
长+宽的和:18÷2= 9(米)
|长/米|8|7|6|…|
|宽/米|1|2|3|…|
|面积/平方米|8|14|18|…|
把各种围法一一列举出来,分别计算出面积,再从中找出面积最大的
规律总结 用一一列举的策略解决问题,要做到有序思考,这样可以不重复、不遗漏,同时还可以对列举出的结果进行比较
用列举的策略解决问题
解题方法
文字列举
袋子中有红球、黄球、蓝球、绿球各一个,从中任意取出两个求,一共有几种情况?
红球—黄球、红球—蓝球、红球—绿球、黄球—蓝球、黄球—绿球、蓝球—绿球
画图列举
或 甲队 乙队 丙队 丁队
方法总结 一一列举时,根据问题选择合适的列举方法,如列表法、文字列举法、画图列举法等
李叔叔要用18根1米长的木条围成一个长方形,怎样围面积最大?是多少平方米?(列一列,找出答案)
长+宽的和:18÷2= 9(米)
|长/米|8|7|6|…|
|宽/米|1|2|3|…|
|面积/平方米|8|14|18|…|
把各种围法一一列举出来,分别计算出面积,再从中找出面积最大的
规律总结 用一一列举的策略解决问题,要做到有序思考,这样可以不重复、不遗漏,同时还可以对列举出的结果进行比较
用列举的策略解决问题
解题方法
文字列举
袋子中有红球、黄球、蓝球、绿球各一个,从中任意取出两个求,一共有几种情况?
红球—黄球、红球—蓝球、红球—绿球、黄球—蓝球、黄球—绿球、蓝球—绿球
画图列举
或 甲队 乙队 丙队 丁队
方法总结 一一列举时,根据问题选择合适的列举方法,如列表法、文字列举法、画图列举法等

答案:
解析:
本题考查的知识点是长方形面积计算及最值问题,通过列举不同长和宽的组合,计算出对应的面积,从而找出面积最大值。
解题方法为先根据长方形周长公式求出长和宽的和,再列举所有可能的长和宽的组合,计算出每种组合下的面积,最后比较得出面积最大的情况。
答案:
长+宽的和:$18÷2 = 9$(米)
列举不同长和宽的组合及对应面积:
|长/米|宽/米|面积/平方米|
| ---- | ---- | ---- |
| 8 | 1 | $8×1 = 8$ |
| 7 | 2 | $7×2 = 14$ |
| 6 | 3 | $6×3 = 18$ |
| 5 | 4 | $5×4 = 20$ |
通过比较可知,当长为5米,宽为4米时,面积最大,最大面积是20平方米。
本题考查的知识点是长方形面积计算及最值问题,通过列举不同长和宽的组合,计算出对应的面积,从而找出面积最大值。
解题方法为先根据长方形周长公式求出长和宽的和,再列举所有可能的长和宽的组合,计算出每种组合下的面积,最后比较得出面积最大的情况。
答案:
长+宽的和:$18÷2 = 9$(米)
列举不同长和宽的组合及对应面积:
|长/米|宽/米|面积/平方米|
| ---- | ---- | ---- |
| 8 | 1 | $8×1 = 8$ |
| 7 | 2 | $7×2 = 14$ |
| 6 | 3 | $6×3 = 18$ |
| 5 | 4 | $5×4 = 20$ |
通过比较可知,当长为5米,宽为4米时,面积最大,最大面积是20平方米。
解题方法 先找出问题的切入点
李叔叔要用18根1米长的木条围成一个长方形,怎样围面积最大?是多少平方米?(列一列,找出答案)
长+宽的和:18÷2= 9(米)
|长/米|8|7|6|…|
|宽/米|1|2|3|…|
|面积/平方米|8|14|18|…|
把各种围法一一列举出来,分别计算出面积,再从中找出面积最大的
规律总结 用一一列举的策略解决问题,要做到有序思考,这样可以不重复、不遗漏,同时还可以对列举出的结果进行比较
用列举的策略解决问题
解题方法
文字列举
袋子中有红球、黄球、蓝球、绿球各一个,从中任意取出两个求,一共有几种情况?
红球—黄球、红球—蓝球、红球—绿球、黄球—蓝球、黄球—绿球、蓝球—绿球
画图列举
或 甲队 乙队 丙队 丁队
方法总结 一一列举时,根据问题选择合适的列举方法,如列表法、文字列举法、画图列举法等

李叔叔要用18根1米长的木条围成一个长方形,怎样围面积最大?是多少平方米?(列一列,找出答案)
长+宽的和:18÷2= 9(米)
|长/米|8|7|6|…|
|宽/米|1|2|3|…|
|面积/平方米|8|14|18|…|
把各种围法一一列举出来,分别计算出面积,再从中找出面积最大的
规律总结 用一一列举的策略解决问题,要做到有序思考,这样可以不重复、不遗漏,同时还可以对列举出的结果进行比较
用列举的策略解决问题
解题方法
文字列举
袋子中有红球、黄球、蓝球、绿球各一个,从中任意取出两个求,一共有几种情况?
红球—黄球、红球—蓝球、红球—绿球、黄球—蓝球、黄球—绿球、蓝球—绿球
画图列举
或 甲队 乙队 丙队 丁队
方法总结 一一列举时,根据问题选择合适的列举方法,如列表法、文字列举法、画图列举法等

答案:
解析:
本题考查的知识点是长方形面积计算及最值问题,通过列举不同长和宽的组合,计算出对应的面积,从而找出面积最大值。
解题方法为先根据长方形周长公式求出长和宽的和,再列举出所有可能的长和宽的组合,计算出每种组合下的面积,最后比较得出面积最大值。
答案:
长+宽的和:$18÷2 = 9$(米)
列举不同长和宽的组合及对应面积:
|长/米|宽/米|面积/平方米|
| ---- | ---- | ---- |
| 8 | 1 | $8×1 = 8$ |
| 7 | 2 | $7×2 = 14$ |
| 6 | 3 | $6×3 = 18$ |
| 5 | 4 | $5×4 = 20$ |
通过比较可知,当长为5米,宽为4米时,面积最大,最大面积是20平方米。
本题考查的知识点是长方形面积计算及最值问题,通过列举不同长和宽的组合,计算出对应的面积,从而找出面积最大值。
解题方法为先根据长方形周长公式求出长和宽的和,再列举出所有可能的长和宽的组合,计算出每种组合下的面积,最后比较得出面积最大值。
答案:
长+宽的和:$18÷2 = 9$(米)
列举不同长和宽的组合及对应面积:
|长/米|宽/米|面积/平方米|
| ---- | ---- | ---- |
| 8 | 1 | $8×1 = 8$ |
| 7 | 2 | $7×2 = 14$ |
| 6 | 3 | $6×3 = 18$ |
| 5 | 4 | $5×4 = 20$ |
通过比较可知,当长为5米,宽为4米时,面积最大,最大面积是20平方米。
查看更多完整答案,请扫码查看


