《2025年实验班提优训练六年级数学上册苏教版》

1. 一根2米长的绳子,用去$\frac{3}{4}$,用去多少米？列式为C。用去$\frac{3}{4}$,还剩多少米？列式为A。用去$\frac{3}{4}$米,还剩多少米？列式为D。
A.$2-2×\frac{3}{4}$
B.$2+2×\frac{3}{4}$
C.$2×\frac{3}{4}$
D.$2-\frac{3}{4}$

答案： 1.C A D 【提示】把这根绳子的长度看作单位“1”，则用去的绳子长度相当于单位“1”的$\frac{3}{4}$，根据“求一个数的几分之几是多少，用乘法计算”列式求解；剩下的绳子长度相当于单位“1”的$(1-\frac{3}{4})$；用去$\frac{3}{4}$米，还剩$(2-\frac{3}{4})$米。

2. 看图列式计算。

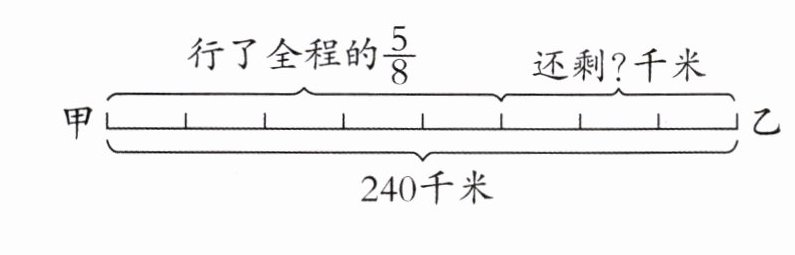
答案： $240-240×\frac{5}{8}=90$(千米)【提示】先求出已经行了多少千米，再用甲、乙两地之间的距离减去已经行的路程就是剩下的路程。

3. 传统文化 中国结 中国结作为中国传统的手工编织工艺品,它有着飘逸雅致的韵味,被认为是团圆、美满、吉祥的象征。为迎接春节,妈妈用一根长6米的红丝带编织中国结,第一天用去全长的$\frac{2}{5}$,第二天用去全长的$\frac{1}{3}$。这根红丝带还剩下多少米？

答案： $6-6×\frac{2}{5}-6×\frac{1}{3}=\frac{8}{5}$(米)【提示】用红丝带的总长度依次减去第一天用去的长度和第二天用去的长度，即可得出还剩下的长度。

4. 惠民超市运来苹果180千克,卖出$\frac{1}{5}$,再卖出多少千克,卖出的就正好是总数的$\frac{1}{3}$？

答案： $180×(\frac{1}{3}-\frac{1}{5})=24$(千克)【提示】这批苹果先卖出了总数的$\frac{1}{5}$，再卖出总数的$(\frac{1}{3}-\frac{1}{5})$，卖出的就正好是总数的$\frac{1}{3}$。

5. 一堆煤有56吨,第一天运走$\frac{3}{8}$,第二天与第一天运走的吨数比是$4:3$。还剩多少吨没运走？

答案： 第二天运走的吨数：$56×\frac{3}{8}÷3×4=28$(吨)第一天与第二天运走总和：$56×\frac{3}{8}+28=49$(吨)还剩：$56-49=7$(吨)【提示】要求还剩多少吨没有运走，就要先求出第二天运走的吨数，即$(56×\frac{3}{8}÷3×4)$吨。还可以换一种思考的角度，即求出剩下的分率。要求剩下的分率，需先求出第二天运走的分率，即$\frac{3}{8}÷3×4=\frac{1}{2}$，剩下的分率为$1-\frac{3}{8}-\frac{1}{2}=\frac{1}{8}$，则剩下的吨数是$56×\frac{1}{8}=7$(吨)。

6. 两根同样长的蜡烛,第一根蜡烛燃烧了它的$\frac{2}{3}$后还剩12厘米；第二根蜡烛燃烧了它的$\frac{3}{4}$后还剩多少厘米？

答案： $12÷(1-\frac{2}{3})×(1-\frac{3}{4})=9$(厘米)【提示】第一根蜡烛燃烧了它的$\frac{2}{3}$后还剩12厘米，那么这12厘米就是蜡烛长度的$(1-\frac{2}{3})$，据此可求出第一根蜡烛的长度；第二根蜡烛的长度和第一根相同，燃烧了它的$\frac{3}{4}$后还剩这根蜡烛的$(1-\frac{3}{4})$，进而可求出剩下长度。

7. 一堆沙子共100吨,第一次运走$\frac{1}{2}$,第二次运走余下部分的$\frac{1}{3}$,第三次运走余下部分的$\frac{1}{4}$……最后一次运走余下部分的$\frac{1}{100}$。这堆沙子还剩下多少吨？

答案： $100×(1-\frac{1}{2})×(1-\frac{1}{3})×(1-\frac{1}{4})×\cdots×(1-\frac{1}{100})=1$(吨)【提示】第一次运走$\frac{1}{2}$，剩下这堆沙子的$(1-\frac{1}{2})$；第二次运走余下部分的$\frac{1}{3}$，剩下这堆沙子的$(1-\frac{1}{2})×(1-\frac{1}{3})$；第三次运走余下部分的$\frac{1}{4}$，剩下这堆沙子的$(1-\frac{1}{2})×(1-\frac{1}{3})×(1-\frac{1}{4})\cdots\cdots$最后一次运走余下部分的$\frac{1}{100}$，还剩下这堆沙子的$(1-\frac{1}{2})×(1-\frac{1}{3})×(1-\frac{1}{4})×\cdots×(1-\frac{1}{100})=\frac{1}{100}$，即剩下$100×\frac{1}{100}=1$(吨)。易错提醒 变化的单位“1”题目中的单位“1”一直在变化，第一次总量是单位“1”，后面的每一次都是前面那一次剩余的量是单位“1”，单位“1”变化的应用题一定要弄清楚每一个分率对应的单位“1”。