《2025年实验班提优训练六年级数学上册苏教版》

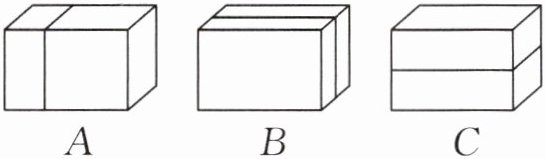
1. 如下图,将一个长方体分割成两个小长方体,按A、B、C三种方式进行分割后,表面积分别增加了12平方厘米、24平方厘米、16平方厘米。原来这个长方体的前面面积是(12)平方厘米;上面面积是(8)平方厘米;右面面积是(6)平方厘米;表面积是(52)平方厘米。

答案： 12 8 6 52 【提示】A 方式分割后增加的面积等于长方体左、右两个面的面积和;B 方式分割后增加的面积等于长方体前、后两个面的面积和;C 方式分割后增加的面积等于长方体上、下两个面的面积和。把增加的三个面积相加所得的和就是长方体的表面积。

2. 有一个长方体木块,从左、右两端分别锯掉一个长3 cm和一个长5 cm的长方体木块后,得到一个正方体木块。这个正方体木块比原来长方体木块的表面积减少了$256cm^2。$原来长方体木块的体积是多少立方厘米?

答案： 256÷4=64(cm²) 64÷(3+5)=8(cm)
(3+5+8)×8×8=1024(cm³)
【提示】分别锯掉一个长 3 cm 和一个长 5 cm 的长方体木块,得到一个正方体木块,说明这个长方体木块的宽和高相等。先根据减少的面积求出原来长方体木块的宽和高,再求出原来长方体木块的体积是多少立方厘米。

3. 一个长方体的宽和高相等,且均为长的一半(如图所示)。将这个长方体平切2刀,竖切3刀,共得到12个长方体,这12个长方体的表面积之和为600平方厘米,求原来长方体的体积。

答案： 设大长方体的宽和高为a厘米,长为2a厘米。
2a×a×6+a×a×8+2a×a×2=600
a²=25 a=5
2×5×5×5=250(立方厘米)
【提示】平切2刀,面积增加4个底面的面积;竖切3刀,面积增加6个右面的面积。

4. 工人师傅把一个底面积是36平方厘米、高是4厘米的长方体钢锭,铸造成一个横截面是边长为5厘米的正方形的长方体零件。铸造后的这个零件长是多少厘米?

答案： 36×4÷(5×5)=5.76(厘米)
【提示】铸造前后物体体积不变,再根据“零件长=体积÷横截面”即可求出答案。

5. 如下图(单位:厘米),有一个长方体容器甲,长30厘米,宽40厘米,高45厘米,里面装满了水。将容器甲中的水倒一部分给另一个长、宽、高分别为45厘米、40厘米和35厘米的长方体空容器乙,使两个容器中的水体积相等。这时容器乙中的水深多少厘米?(容器厚度忽略不计)

答案： 30÷2=15(厘米)
【提示】假设以容器甲的右面为底面,将容器甲翻过来,就成了长 45 厘米、宽 40 厘米、高 30 厘米的长方体,底面积与容器乙一样大,要使两个容器内的水体积相等,高应为原来的一半。