第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 小宇家有两块长8分米、宽5分米的玻璃,两块长6分米、宽5分米的玻璃,他想做一个无盖的鱼缸,则还要配一块长(
8
)分米、宽(6
)分米的玻璃,做成的鱼缸的容积是(240
)升。(玻璃的厚度忽略不计)
答案:
8 6 240 【提示】根据长方体的特征,可知做的这个玻璃鱼缸的长为8分米,宽为6分米,高为5分米,因此要配一块长为8分米、宽为6分米的玻璃。
2. 一个长方体的长、宽、高分别是a米、b米、h米。若高增加2米,则新长方体的体积比原来长方体的体积增加(
2ab
)立方米。
答案:
2ab 【提示】体积增加的部分是长a米、宽b米、高2米的长方体的体积。
3. 有一个棱长是4分米的正方体零件,从它一个面的正中间向对面挖去一个底面边长是1分米的正方形的小长方体(如图),这个零件的表面积(
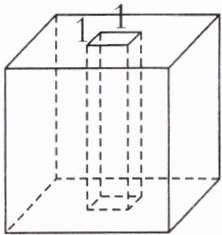
A.增加了14平方分米
B.减少了14平方分米
C.增加了16平方分米
D.减少了16平方分米
A
)。
A.增加了14平方分米
B.减少了14平方分米
C.增加了16平方分米
D.减少了16平方分米
答案:
A 【提示】观察题图可知,这个零件的表面积挖去部分增加了4×1×4=16(平方分米),上、下底面减少了1×1×2=2(平方分米),因此这个零件的表面积共增加了16-2=14(平方分米)。
4. 如下图,一个长方体玻璃水槽被一块玻璃分成A、B两部分。A的底面积为$30dm^2,B$的底面积为$20dm^2,$水槽的高为8dm。B部分水槽中装满水,A部分水槽里水的高度为3dm,现将中间玻璃抽出后,水槽里水的高度为(
5
)dm。(玻璃厚度忽略不计)
答案:
5 【提示】根据长方体的容积(体积)公式:V=Sh,可求出这个水槽共装水30×3+20×8=250(dm³),然后用水的体积除以整个长方体水槽的底面积即可。
5. 如图,用混凝土浇筑一个无盖的长方体水槽(底面也浇筑),从外面量,长14分米,宽7分米,高5分米,混凝土厚1分米。浇筑这个水槽一共要用多少立方分米混凝土?


答案:
(14-1×2)×(7-1×2)×(5-1)=240(立方分米)14×7×5-240=250(立方分米)【提示】用长14分米、宽7分米、高5分米的长方体的体积减去长(14-1×2)分米、宽(7-1×2)分米、高(5-1)分米的长方体的体积即可求解。
6. 下图是一个裹成正方体的油布(每两层之间没有缝隙),中间的卷轴横截面是正方形,边长为20厘米,把这个油布平展开来,每层的厚度是4毫米。全部拉开,长多少米?


答案:
20厘米=2分米 4毫米=0.04分米(8×8×8-2×2×8)÷(8×0.04)=1500(分米)1500分米=150米【提示】先求出油布的体积,再用油布的体积除以油布的横截面面积,即可求出油布的长。
7. 实验班原创 几何直观 某超市买来一种饮料若干箱,长方体箱子高1分米,底面是边长3分米的正方形,现将这些饮料箱由下往上堆成长方体,如右图。

[我思考] 堆成的长方体的表面积与(
[我验证] 填写下表。

[我发现] 当饮料箱的个数是m时,堆成长方体的表面积是(

[我思考] 堆成的长方体的表面积与(
饮料箱
)的个数有关。[我验证] 填写下表。

[我发现] 当饮料箱的个数是m时,堆成长方体的表面积是(
18+12m
)平方分米。
答案:
饮料箱 66 78 18+12m 【提示】每增加1箱,表面积就增加12平方分米。
查看更多完整答案,请扫码查看


