8. 转化思想 如图,在半径为5的扇形AOB中,$∠AOB= 90^{\circ }$,C是$\widehat {AB}$上一点,$CD⊥OA,CE⊥OB$,垂足分别为D、E,若$CD= CE$,则图中阴影部分面积为( ).
A.$\frac {25π}{16}$
B.$\frac {25π}{8}$
C.$\frac {25π}{6}$
D.$\frac {25π}{4}$
A.$\frac {25π}{16}$
B.$\frac {25π}{8}$
C.$\frac {25π}{6}$
D.$\frac {25π}{4}$
答案:
B[解析]连接OC,如图所示.

∵∠AOB=90°,CD⊥OA,CE⊥OB,
∴∠AOB=∠ODC=∠OEC=90°,
∴四边形OECD是矩形.
∵CD=CE,
∴四边形OECD是正方形,
∴∠DCE=90°,△DCE和△OEC全等,
∴S阴影=S△DCE+S半弓形BCE=S△OCE+S半弓形BCE=S扇形COB=$\frac{45\pi×5^2}{360}$=$\frac{25\pi}{8}$.故选B.
知识拓展 求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积,求阴影面积常用的方法:①直接用公式法;②和差法;③割补法.
B[解析]连接OC,如图所示.

∵∠AOB=90°,CD⊥OA,CE⊥OB,
∴∠AOB=∠ODC=∠OEC=90°,
∴四边形OECD是矩形.
∵CD=CE,
∴四边形OECD是正方形,
∴∠DCE=90°,△DCE和△OEC全等,
∴S阴影=S△DCE+S半弓形BCE=S△OCE+S半弓形BCE=S扇形COB=$\frac{45\pi×5^2}{360}$=$\frac{25\pi}{8}$.故选B.
知识拓展 求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积,求阴影面积常用的方法:①直接用公式法;②和差法;③割补法.
9. 用准确的文字语言描述“垂径定理”:垂直于弦的直径平分______.
答案:
弦以及弦所对的两条弧
10. 正十二边形的一个内角的度数为______.
答案:
150°
11. 如图,AB、AC是$\odot O$的弦,过点A的切线交CB的延长线于点D,若$∠BAD= 35^{\circ }$,则$∠C= $______$^{\circ }$.


答案:
35
12. 将量角器按如图所示的方式放置在三角形纸板上,使顶点C在半圆上,点A、B的读数分别为$100^{\circ }$、$150^{\circ }$,则$∠ACB$的大小为______$^{\circ }$.
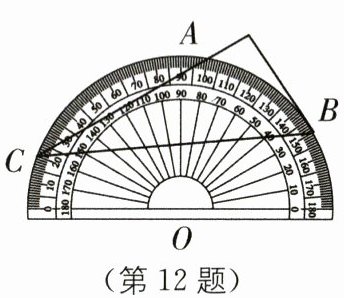

答案:
25
13. (2025·无锡经开区期末)已知圆锥的母线长为5 cm,底面半径为3 cm,则此圆锥的侧面积为______$cm^{2}$.
答案:
15π
14. 如图,在$\odot O$中,直径AB与弦CD交于点E.$\widehat {AC}= 2\widehat {BD}$,连接AD,过点B的切线与AD的延长线交于点F.若$∠AFB= 68^{\circ }$,则$∠DEB= $______$^{\circ }$.


答案:
66° [解析]连接OC、OD.
∵BF是$\odot O$的切线,AB是$\odot O$的直径,
∴OB⊥BF,
∴∠ABF=90°.
∵∠AFB=68°,
∴∠BAF=90°−∠AFB=22°,
∴∠BOD=2∠BAF=44°.
∵$\overset{\frown}{AC}=2\overset{\frown}{BD}$,
∴∠COA=2∠BOD=88°,
∴∠CDA=$\frac{1}{2}$∠COA=44°.
∵∠DEB是△AED的一个外角,
∴∠DEB=∠BAF+∠CDA=66°.
∵BF是$\odot O$的切线,AB是$\odot O$的直径,
∴OB⊥BF,
∴∠ABF=90°.
∵∠AFB=68°,
∴∠BAF=90°−∠AFB=22°,
∴∠BOD=2∠BAF=44°.
∵$\overset{\frown}{AC}=2\overset{\frown}{BD}$,
∴∠COA=2∠BOD=88°,
∴∠CDA=$\frac{1}{2}$∠COA=44°.
∵∠DEB是△AED的一个外角,
∴∠DEB=∠BAF+∠CDA=66°.
15. 如图,在正八边形ABCDEFGH中,若四边形BCFG的面积是$12cm^{2}$,则正八边形的面积为______$cm^{2}$.


答案:
24
16. 如图,将一个等腰直角三角形ABC的直角顶点C放在$\odot O$上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在$\odot O上截得的线段DE= 2cm$,且$BC= 7cm$,则OC的长为______cm.


答案:
3 [解析]如图,过点O作OM⊥AB,
∴DM=$\frac{1}{2}$DE=1cm.
设MO=hcm,CO=DO=xcm,
∵△ABC为等腰直角三角形,AC=BC,
∴∠MAO=45°,
∴△AOM是等腰直角三角形,
∴AO=$\sqrt{2}$MO=$\sqrt{2}$h(cm).
∵AO=(7−x)cm,
∴$\sqrt{2}$h=7−x,
∴2h²=49−14x+x².
在Rt△DMO中,由勾股定理,得h²=x²−1²,
∴2x²−2=49−14x+x²,解得x1=−17(不符合题意,舍去),x2=3,
∴OC=3cm.

3 [解析]如图,过点O作OM⊥AB,
∴DM=$\frac{1}{2}$DE=1cm.
设MO=hcm,CO=DO=xcm,
∵△ABC为等腰直角三角形,AC=BC,
∴∠MAO=45°,
∴△AOM是等腰直角三角形,
∴AO=$\sqrt{2}$MO=$\sqrt{2}$h(cm).
∵AO=(7−x)cm,
∴$\sqrt{2}$h=7−x,
∴2h²=49−14x+x².
在Rt△DMO中,由勾股定理,得h²=x²−1²,
∴2x²−2=49−14x+x²,解得x1=−17(不符合题意,舍去),x2=3,
∴OC=3cm.

17. 如图,将半径为2,圆心角为$120^{\circ }$的扇形OAB绕点A逆时针旋转$60^{\circ }$,点O、B的对应点分别为$O'$、$B'$,连接$BB'$,则图中阴影部分的面积是______.
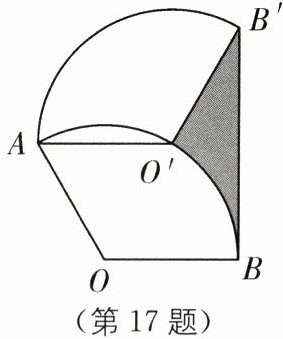

答案:
$2\sqrt{3}-\frac{2\pi}{3}$
18. 手拉手模型 $\triangle ABC$是边长为5的等边三角形,$\triangle DCE$是边长为3的等边三角形,直线BD与直线AE交于点F.如图,若点D在$\triangle ABC$内,$∠DBC= 20^{\circ }$,则$∠BAF= $______$^{\circ }$;现将$\triangle DCE$绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是______.
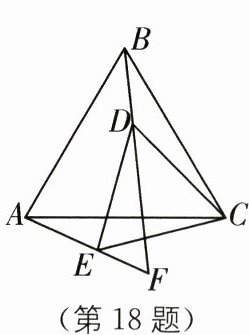

答案:
80 $4-\sqrt{3}$ [解析]
∵△ACB、△DEC都是等边三角形,
∴AC=CB,DC=EC,∠ACB=∠DCE=60°,
∴∠BCD=∠ACE.
在△BCD和△ACE中,$\begin{cases} CB=CA, \\ ∠BCD=∠ACE, \\ CD=CE, \end{cases}$
∴△BCD≌△ACE(SAS),
∴∠DBC=∠EAC=20°.
∵∠BAC=60°,
∴∠BAF=∠BAC+∠CAE=80°.
如图,设BF交AC于点T.
∵△BCD≌△ACE,
∴∠CBD=∠CAF.
∵∠BTC=∠ATF,
∴∠ACB=∠AFB=60°,
∴点F
在△ABC的外接圆上运动.
当∠ABF最小时,AF的值最小,

此时CD⊥BD,
∴BD=$\sqrt{BC^2-CD^2}=\sqrt{5^2-3^2}$=4,
∴AE=BD=4,∠BDC=∠AEC=90°.
∵CD=CE,CF=CF,
∴Rt△CFD≌Rt△CFE(HL),
∴∠DCF=∠ECF=30°,
∴EF=$\sqrt{3}$,
∴AF的最小值=AE-EF=$4-\sqrt{3}$.
80 $4-\sqrt{3}$ [解析]
∵△ACB、△DEC都是等边三角形,
∴AC=CB,DC=EC,∠ACB=∠DCE=60°,
∴∠BCD=∠ACE.
在△BCD和△ACE中,$\begin{cases} CB=CA, \\ ∠BCD=∠ACE, \\ CD=CE, \end{cases}$
∴△BCD≌△ACE(SAS),
∴∠DBC=∠EAC=20°.
∵∠BAC=60°,
∴∠BAF=∠BAC+∠CAE=80°.
如图,设BF交AC于点T.
∵△BCD≌△ACE,
∴∠CBD=∠CAF.
∵∠BTC=∠ATF,
∴∠ACB=∠AFB=60°,
∴点F
在△ABC的外接圆上运动.
当∠ABF最小时,AF的值最小,

此时CD⊥BD,
∴BD=$\sqrt{BC^2-CD^2}=\sqrt{5^2-3^2}$=4,
∴AE=BD=4,∠BDC=∠AEC=90°.
∵CD=CE,CF=CF,
∴Rt△CFD≌Rt△CFE(HL),
∴∠DCF=∠ECF=30°,
∴EF=$\sqrt{3}$,
∴AF的最小值=AE-EF=$4-\sqrt{3}$.
查看更多完整答案,请扫码查看


