《2025年课时训练九年级数学上册苏科版江苏人民出版社》

  2. 面积问题:利用三角形、矩形的____公式,建立等量关系列一元二次方程.

答案： 面积

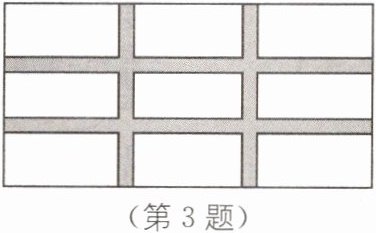
3. 如图,在长为100m,宽为50m的矩形空地上修筑四条宽度相等的小路,若余下的部分全部种上花卉,且花圃的面积是$3600m^2,$则小路的宽是( ).

A.5m
B.70m
C.5m或70m
D.10m

答案： A

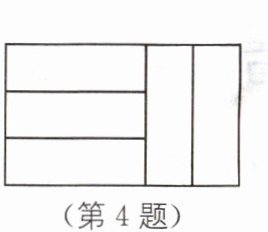
4. 五个完全相同的小长方形拼成如图所示的大长方形,大长方形的面积是$135cm^2,$则以小长方形的宽为边长的正方形面积是$____cm^2.$

答案： 9

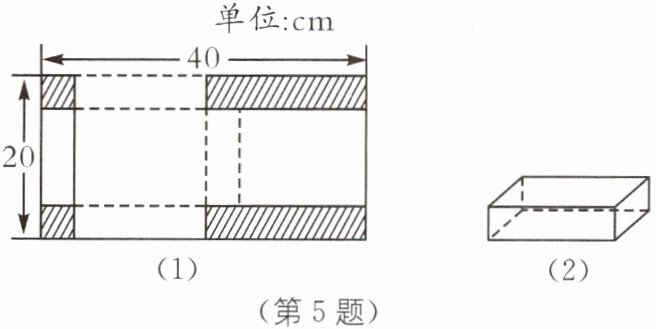
5. 提分优练 中考新考法 操作探究 如图(1),有一张长40cm、宽20cm的长方形硬纸片,裁去角上2个小正方形和2个小长方形(图中阴影部分)之后,恰好折成如图(2)的有盖纸盒.
(1)若纸盒的高是3cm,求纸盒底面长方形的长和宽;
(2)若纸盒的底面积是$150cm^2,$求纸盒的高.

答案：
(1)由题意,得纸盒底面长方形的长为(40-2×3)÷2=17(cm),纸盒底面长方形的宽为20-2×3=14(cm).故纸盒底面长方形的长为17 cm,宽为14 cm.
(2)设当纸盒的高为x cm时,纸盒的底面积是150cm².依题意,得$\frac{(40-2x)}{2}$×(20-2x)=150,化简,得$x^{2}-30x+125=0$,解得$x_{1}=5$,$x_{2}=25$.当x=5时,20-2x=10＞0,符合题意;当x=25时,20-2x=-30＜0,不符合题意,舍去.故若纸盒的底面积是150cm²,纸盒的高为5 cm.

1. 平均变化率问题：$a(1\pm x)^{n}= b$,其中____为基础量,____为增长(或降低)的次数,____为增长(或降低)的百分数,____为$a$增长(或降低)$n$次的结果。

答案： a n x b

 2. 储蓄问题：本息和= 本金+____= 本金+本金×利率×____= 本金$(1+$利率×____)。

答案： 利息 期数 期数

3. 某市决定改善城市容貌,绿化环境,计划经过两年时间,绿地面积增加44%,这两年平均每年绿地面积的增长率是( )。

A.20%
B.11%
C.22%
D.44%

答案： A

4. (2025·江阴期末)某商品经过两次降价,售价由原来的每件25元降到每件16元,已知两次降价的百分率相同,设平均每次降价的百分率为$x$,可列方程为( )。

A.$25(1-x)^{2}= 16$
B.$25(1+x)^{2}= 16$
C.$25(1-2x)= 16$
D.$25(1+2x)= 16$

答案： A

5. 新情境 数学与生活融合 某校“研学”活动小组在一次野外实践时,发现一种植物的1个主干上长出$x$个枝干,每个枝干上再长出$x$个小分支.若在1个主干上的主干、枝干和小分支的数量之和是31个,则$x$等于( )。

A.4
B.5
C.6
D.7

答案： B [解析]依题意,得$1+x+x^{2}=31$,整理,得$x^{2}+x-30=0$,解得$x_{1}=5$,$x_{2}=-6$(不合题意,舍去).故选B.