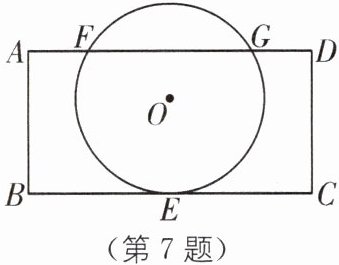
7. 提分优练 (南京十三中特长生)四边形 $ A B C D $ 是矩形,$ \odot O $ 与 $ B C $ 相切于点 $ E $,且 $ E $ 为 $ B C $ 中点,$ A B = 3 $,$ B C = 6 $,$ A F = 3 - \sqrt { 3 } $。
(1)求 $ \odot O $ 的半径。
(2)若矩形 $ A B C D $ 绕点 $ E $ 顺时针旋转 $ \alpha ^ { \circ } $ ($ 0 < \alpha \leq 180 $),是否存在 $ \odot O $ 与矩形的一边相切?若存在,求出旋转角;若不存在,说明理由。
(1)求 $ \odot O $ 的半径。
(2)若矩形 $ A B C D $ 绕点 $ E $ 顺时针旋转 $ \alpha ^ { \circ } $ ($ 0 < \alpha \leq 180 $),是否存在 $ \odot O $ 与矩形的一边相切?若存在,求出旋转角;若不存在,说明理由。

答案:
(1)如图
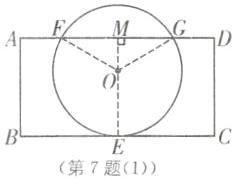
(1),连接$OF$、$OG$,连接$EO$并延长交$FG$于点$M$.设$\odot O$的半径为$r$,则$OE=OF=OG=r$,$OM\perp FG$,$OM=3 - r$,$AM=BE=3$,$\therefore FM=AM - AF=\sqrt{3}$.
在$Rt\triangle OFM$中,$(3 - r)^2+(\sqrt{3})^2=r^2$,解得$r = 2$,$\therefore\odot O$的半径为2.
(2)存在,$\alpha$为$30^\circ$、$60^\circ$或$180^\circ$.理由如下:
如图
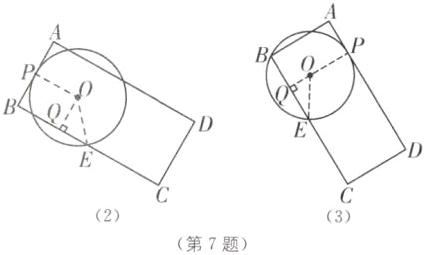
(2),当$AB$与$\odot O$相切时,设切点为$P$,连接$OP$、$OE$,则$OP=OE=2$,$BE=3$.过点$O$作$OQ\perp BE$,垂足为$Q$,则$BQ=2$,$EQ=1$,$\therefore\angle OEQ=60^\circ$,$\therefore\alpha=30^\circ$;
如图
(3),当$AD$与$\odot O$相切时,同理$OQ=1$,$OE=2$,$\angle OEB=30^\circ$,$\therefore\alpha=60^\circ$.
当$\alpha=180^\circ$时,$BC$与$\odot O$相切.
综上$\alpha=30^\circ$、$60^\circ$或$180^\circ$.
(1)如图
(1),连接$OF$、$OG$,连接$EO$并延长交$FG$于点$M$.设$\odot O$的半径为$r$,则$OE=OF=OG=r$,$OM\perp FG$,$OM=3 - r$,$AM=BE=3$,$\therefore FM=AM - AF=\sqrt{3}$.
在$Rt\triangle OFM$中,$(3 - r)^2+(\sqrt{3})^2=r^2$,解得$r = 2$,$\therefore\odot O$的半径为2.

(2)存在,$\alpha$为$30^\circ$、$60^\circ$或$180^\circ$.理由如下:
如图
(2),当$AB$与$\odot O$相切时,设切点为$P$,连接$OP$、$OE$,则$OP=OE=2$,$BE=3$.过点$O$作$OQ\perp BE$,垂足为$Q$,则$BQ=2$,$EQ=1$,$\therefore\angle OEQ=60^\circ$,$\therefore\alpha=30^\circ$;

如图
(3),当$AD$与$\odot O$相切时,同理$OQ=1$,$OE=2$,$\angle OEB=30^\circ$,$\therefore\alpha=60^\circ$.
当$\alpha=180^\circ$时,$BC$与$\odot O$相切.
综上$\alpha=30^\circ$、$60^\circ$或$180^\circ$.
1. 圆锥的基本规律:圆锥的侧面展开图是扇形,其半径等于圆锥的____,弧长等于圆锥的底面圆____。
答案:
母线长 周长
2. 圆锥的侧面积计算公式:母线长为 $ l $,底面圆半径为 $ r $ 的圆锥的侧面积为 $ S_{侧面} = $____。
答案:
$\pi rl$
3. 圆锥的全面积计算公式:$ S_{圆锥全} = \pi rl + $____。
答案:
$\pi r^2$
4. 圆锥的底面半径 $ r $、母线长 $ l $、侧面展开图的圆心角度数 $ n $ 之间的关系:
$ \because $____,$ \therefore \frac{r}{l} = $____。
$ \because $____,$ \therefore \frac{r}{l} = $____。
答案:
$2\pi r=\frac{n\pi l}{180}$ $\frac{n}{360}$
5. (2024·无锡中考)已知圆锥的底面圆半径为 3,母线长为 4,则圆锥的侧面积为( )。
A.$ 6\pi $
B.$ 12\pi $
C.$ 15\pi $
D.$ 24\pi $
A.$ 6\pi $
B.$ 12\pi $
C.$ 15\pi $
D.$ 24\pi $
答案:
B
6. 已知一个圆锥的母线长为 10 cm,将侧面展开后所得扇形的圆心角是 $ 144^{\circ} $,则这个圆锥的底面圆的半径是____cm。
答案:
4 [解析]设圆锥底面圆的半径为$r$ cm,那么圆锥底面圆周长为$2\pi r$ cm,又圆锥侧面展开后的弧长为$\frac{144\pi×10}{180}$ cm,则$2\pi r=\frac{144\pi×10}{180}$,解得$r = 4$.
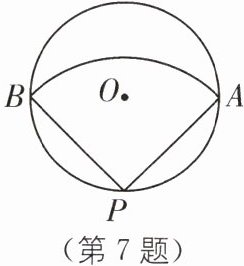
7. 提分优练 中考新考法 操作探究 如图,在一个半径为 $ 2\sqrt{2} $ 的圆形纸片中,剪一个圆心角为 $ 90^{\circ} $ 的扇形。
(1)求这个扇形的面积(结果保留 $ \pi $);
(2)用所剪的纸片围成一个圆锥的侧面,求这个圆锥的底面圆的半径。
(1)求这个扇形的面积(结果保留 $ \pi $);
(2)用所剪的纸片围成一个圆锥的侧面,求这个圆锥的底面圆的半径。

答案:
(1)如图,连接AB.

∵∠APB = 90°,
∴AB为⊙O的直径.
∵APB为扇形,
∴PA = PB,
∴△PAB为等腰直角三角形,
∴PA = $\frac{\sqrt{2}}{2}$AB = $\frac{\sqrt{2}}{2}$×4$\sqrt{2}$ = 4,
∴这个扇形的面积 = $\frac{90\pi×4^2}{360}$ = 4π.
(2)设这个圆锥的底面圆的半径为$r$.
∵弧AB的长 = $\frac{90\pi×4}{180}$ = 2πr,
∴2πr = 2π,解得$r = 1$.
即这个圆锥的底面圆的半径为1.
(1)如图,连接AB.

∵∠APB = 90°,
∴AB为⊙O的直径.
∵APB为扇形,
∴PA = PB,
∴△PAB为等腰直角三角形,
∴PA = $\frac{\sqrt{2}}{2}$AB = $\frac{\sqrt{2}}{2}$×4$\sqrt{2}$ = 4,
∴这个扇形的面积 = $\frac{90\pi×4^2}{360}$ = 4π.
(2)设这个圆锥的底面圆的半径为$r$.
∵弧AB的长 = $\frac{90\pi×4}{180}$ = 2πr,
∴2πr = 2π,解得$r = 1$.
即这个圆锥的底面圆的半径为1.
查看更多完整答案,请扫码查看


