7. 如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若$∠ADB= 20^{\circ }$,则这个正多边形的边数为____.


答案:
九
8. (2025·盐城大丰区期中)正六边形ABCDEF的边长为4,求对角线AC的长和正六边形的面积.


答案:
∵AB=BC=CD=4,∠B=∠BCD=120°,
∴∠ACB=∠BAC=30°,
∴∠ACD=90°.
利用等边对等角求出∠ACB的度数,从而得出∠ACD的度数
∵∠CDA=∠EDA=60°,
∴∠CAD=30°,
∴AD=2CD=8,
∴AC=√3CD=4√3
如图,设圆心为O,
连接OC,作OG⊥CD于点G,

∴OG=1/2AC=2√3,
∴S△OCD=1/2·CD·OG=1/2×4×2√3=4√3,
∴正六边形的面积=6×4√3=24√3.
∵AB=BC=CD=4,∠B=∠BCD=120°,
∴∠ACB=∠BAC=30°,
∴∠ACD=90°.
利用等边对等角求出∠ACB的度数,从而得出∠ACD的度数
∵∠CDA=∠EDA=60°,
∴∠CAD=30°,
∴AD=2CD=8,
∴AC=√3CD=4√3
如图,设圆心为O,
连接OC,作OG⊥CD于点G,

∴OG=1/2AC=2√3,
∴S△OCD=1/2·CD·OG=1/2×4×2√3=4√3,
∴正六边形的面积=6×4√3=24√3.
9. 提分优练 如图,$\odot O$半径为4cm,正六边形ABCDEF为其内接正六边形,点P、Q同时分别从A、D两点出发,以1cm/s的速度沿AF、DC向终点F、C运动,连接PB、QE、PE、BQ. 设运动时间为t s.
(1)求证:四边形PEQB为平行四边形.
(2)填空:
①当$t= $____时,四边形PBQE为菱形;
②当$t= $____时,四边形PBQE为矩形.

(1)求证:四边形PEQB为平行四边形.
(2)填空:
①当$t= $____时,四边形PBQE为菱形;
②当$t= $____时,四边形PBQE为矩形.

答案:
(1)
∵正六边形ABCDEF内接于⊙O,
∴AB=BC=CD=DE=EF=FA,
∠A=∠ABC=∠C=∠D=∠DEF=∠F.
∵点P、Q同时分别从A、D两点出发,以1cm/s的速度沿AF、DC向终点F、C运动,
∴AP=DQ=tcm,PF=QC=(4−t)cm.
在△ABP和△DEQ中,{AB=DE,∠A=∠D,AP=DQ}
∴△ABP≌△DEQ(SAS),
∴BP=EQ.
同理可证PE=QB.
∴四边形PEQB为平行四边形.
(2)①2 [解析]当PA=PF,QC=QD时,四边形PBQE为菱形,此时t=2.
②0或4 [解析]当t=0时,∠EPF=∠PEF=30°,
不要忘了考虑t=0的情况
∴∠BPE=120°−30°=90°,
∴此时四边形PBQE为矩形.
当t=4时,同理可知∠BPE=90°,
此时四边形PBQE为矩形.
综上,当t=0或4时,四边形PBQE为矩形.
(1)
∵正六边形ABCDEF内接于⊙O,
∴AB=BC=CD=DE=EF=FA,
∠A=∠ABC=∠C=∠D=∠DEF=∠F.
∵点P、Q同时分别从A、D两点出发,以1cm/s的速度沿AF、DC向终点F、C运动,
∴AP=DQ=tcm,PF=QC=(4−t)cm.
在△ABP和△DEQ中,{AB=DE,∠A=∠D,AP=DQ}
∴△ABP≌△DEQ(SAS),
∴BP=EQ.
同理可证PE=QB.
∴四边形PEQB为平行四边形.
(2)①2 [解析]当PA=PF,QC=QD时,四边形PBQE为菱形,此时t=2.
②0或4 [解析]当t=0时,∠EPF=∠PEF=30°,
不要忘了考虑t=0的情况
∴∠BPE=120°−30°=90°,
∴此时四边形PBQE为矩形.
当t=4时,同理可知∠BPE=90°,
此时四边形PBQE为矩形.
综上,当t=0或4时,四边形PBQE为矩形.
1. 弧长的计算公式:如果弧长为 $ l $,弧所对圆心角度数为 $ n $,弧所在圆的半径为 $ R $,那么弧长 $ l = $____。
答案:
$\frac{n\pi R}{180}$
2. 扇形面积的计算公式:(1)圆心角度数为 $ n $、半径为 $ R $ 的扇形面积 $ S = $____;(2)弧长为 $ l $、半径为 $ R $ 的扇形面积 $ S = $____。
答案:
(1)$\frac{n\pi R^2}{360}$
(2)$\frac{1}{2}lR$
(1)$\frac{n\pi R^2}{360}$
(2)$\frac{1}{2}lR$
3. 半径为 6,圆心角为 $ 60 ^ { \circ } $ 的弧长为( )。
A.6
B.$ 3 \pi $
C.$ 2 \pi $
D.$ 4 \pi $
A.6
B.$ 3 \pi $
C.$ 2 \pi $
D.$ 4 \pi $
答案:
C
4. 如图,$ OA $ 是 $ \odot O $ 的半径,弦 $ BC \perp OA $,垂足为 $ M $,连接 $ OB $、$ AC $,如果 $ OB // AC $,$ OB = 2 $,那么图中阴影部分的面积是( )。
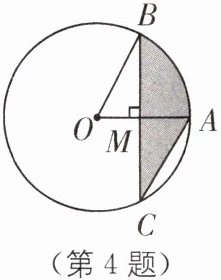
A.$ \frac { 1 } { 3 } \pi $
B.$ \frac { 2 } { 3 } \pi $
C.$ \pi $
D.$ 2 \pi $

A.$ \frac { 1 } { 3 } \pi $
B.$ \frac { 2 } { 3 } \pi $
C.$ \pi $
D.$ 2 \pi $
答案:
B
5. 如图,半圆 $ O $ 的直径 $ AD = 8 \mathrm { cm } $,$ B $、$ C $ 是半圆上的两点,且 $ \angle ABC = 110 ^ { \circ } $,则 $ \overgroup { C D } $ 的长度为____ $ \mathrm { cm } $。
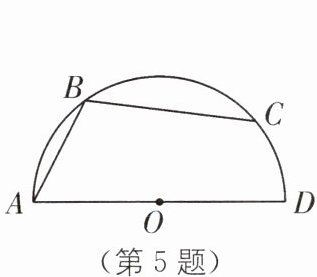

答案:
$\frac{8\pi}{9}$
6. 中考新考法 操作探究 如图,一扇形纸扇完全打开后,$ AB $ 和 $ AC $ 的夹角为 $ 120 ^ { \circ } $,$ AB $ 长为 $ 25 \mathrm { cm } $,贴纸部分的宽 $ BD $ 为 $ 15 \mathrm { cm } $。
(1)求 $ \overgroup { B C } $ 的长度;
(2)求纸扇上贴纸部分的面积。

(1)求 $ \overgroup { B C } $ 的长度;
(2)求纸扇上贴纸部分的面积。

答案:
(1)$\overset{\frown}{BC}$的长度$=\frac{120×\pi×25}{180}=\frac{50}{3}\pi(cm)$.
(2)$\because AB=25\ cm,BD=15\ cm,\therefore AD=25 - 15 = 10(cm)$.
$\because S_{扇形ABC}=\frac{120×\pi×25^2}{360}=\frac{625\pi}{3}(cm^2)$,$S_{扇形ADE}=\frac{120\pi×10^2}{360}=\frac{100\pi}{3}(cm^2)$,$\therefore$贴纸部分的面积$=\frac{625\pi}{3}-\frac{100\pi}{3}=175\pi(cm^2)$.
(1)$\overset{\frown}{BC}$的长度$=\frac{120×\pi×25}{180}=\frac{50}{3}\pi(cm)$.
(2)$\because AB=25\ cm,BD=15\ cm,\therefore AD=25 - 15 = 10(cm)$.
$\because S_{扇形ABC}=\frac{120×\pi×25^2}{360}=\frac{625\pi}{3}(cm^2)$,$S_{扇形ADE}=\frac{120\pi×10^2}{360}=\frac{100\pi}{3}(cm^2)$,$\therefore$贴纸部分的面积$=\frac{625\pi}{3}-\frac{100\pi}{3}=175\pi(cm^2)$.
查看更多完整答案,请扫码查看


