10. 方程$x^{2}-2x+m= 0$有两个相等的实数根,则m的值为____.
答案:
1
11. 关于x的一元二次方程$ax^{2}+bx-2024= 0的一个根为x= 1$,写出满足条件的实数a、b的值____.
答案:
a=2024,b=0(答案不唯一,只要a≠0且a+b=2024即可)
12. 方程$x^{2}-5x-1= 0$的根的判别式的值为____.
答案:
29
13. 已知$a≠0,a≠b,x= 1是方程ax^{2}+bx-10= 0$的一个解,则$\frac {a^{2}-b^{2}}{2a-2b}$的值是____.
答案:
5
14. (2024·常州期中)已知等腰三角形ABC的边长分别是m、n、4,且m、n是关于x的方程$x^{2}-6x+a+1= 0$的两根.则a的值为____.
答案:
7或8 [解析]当m≠n时,将x=4代入原方程,得4²-6×4+a+1=0,解得a=7,此时原方程为x²-6x+8=0,解得m=2,n=4.
∵2+4=6>4,
∴2、4、4能组成三角形,a=7符合题意;当m=n时,Δ=(-6)²-4×1×(a+1)=0,解得a=8,此时原方程为x²-6x+9=0,解得m=n=3.
∵3+3=6>4,
∴3、3、4能组成三角形,a=8符合题意.综上所述,a的值为7或8.思路引导 本题考查了根的判别式、一元二次方程的解、三角形的三边关系以及等腰三角形的性质,分m≠n及m=n两种情况,求出a值是解题的关键.
∵2+4=6>4,
∴2、4、4能组成三角形,a=7符合题意;当m=n时,Δ=(-6)²-4×1×(a+1)=0,解得a=8,此时原方程为x²-6x+9=0,解得m=n=3.
∵3+3=6>4,
∴3、3、4能组成三角形,a=8符合题意.综上所述,a的值为7或8.思路引导 本题考查了根的判别式、一元二次方程的解、三角形的三边关系以及等腰三角形的性质,分m≠n及m=n两种情况,求出a值是解题的关键.
15. 观察表格,一元二次方程$x^{2}+(2k+1)x+k^{2}-2= 0最精确的一个近似解x= $____(精确到0.1).
|x|1.3|1.4|1.5|1.6|1.7|1.8|1.9|
|$x^{2}+(2k+1)x+k^{2}-2$|-0.61|-0.44|-0.25|-0.04|0.19|0.44|0.71|

|x|1.3|1.4|1.5|1.6|1.7|1.8|1.9|
|$x^{2}+(2k+1)x+k^{2}-2$|-0.61|-0.44|-0.25|-0.04|0.19|0.44|0.71|

答案:
1.6
16. 某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.经调查,售价在40元至60元范围内,这种台灯的售价每上涨1元,其销售量就将减少10个.为实现平均每月10000元的销售利润,则这种台灯的售价应定为____元.
答案:
50 [解析]设售价应定为x元,则(x-30)[600-10(x-40)]=10000,整理,得x²-130x+4000=0,解得x₁=50,x₂=80(不符合题意,舍去).
17. 跨学科 古诗词理解 《念奴娇·赤壁怀古》,在苏轼笔下,周瑜年少有为,文采风流,雄姿英发,谈笑间,樯橹灰飞烟灭,然天妒英才,英年早逝,欣赏下面改编的诗歌,“大江东去浪淘尽,千古风流数人物.而立之年督东吴,早逝英年两位数.十位恰小个位三,个位平方与寿符.”则这位风流人物去世的年龄为____岁.
答案:
36 [解析]设这位风流人物去世的年龄十位数字为x,则个位数字为x+3,则根据题意10x+(x+3)=(x+3)²,整理得x²-5x+6=0,解得x₁=2,x₂=3.由题意,而立之年督东吴,则x=2舍去,
∴这位风流人物去世的年龄为36岁.
∴这位风流人物去世的年龄为36岁.
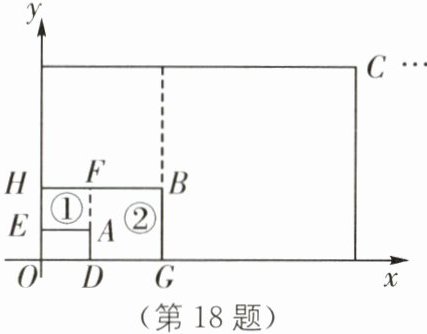
18. 如图,在平面直角坐标系中,以第一个矩形ODAE的边AE为边向上作正方形①,以DF为边向右作正方形②,得到第二个矩形OGBH,以此类推,得到第3个矩形、第4个矩形,…,若这些矩形右上角的顶点A、B、C、…与原点O在同一直线上,则这条直线的函数表达式为____.

答案:
y= $\frac{\sqrt{5}-1}{2}x$ [解析]
∵这些矩形右上角的顶点A、B、C…与原点O在同一直线上,
∴可设这条直线的函数表达式为y=kx(k>0),设OD=a,AD=b,则DF=BG=a+b,OG=2a+b,
∴A(a,b),B(2a+b,a+b).将点A、B的坐标代入y=kx(k≠0),得$\begin{cases}b=ak①,\\a+b=k(2a+b)②,\end{cases}$把①代入②,得a+ak=k(2a+ak),化简,得k²+k-1=0,解得k= $\frac{\sqrt{5}-1}{2}$或k= $\frac{-\sqrt{5}-1}{2}$(舍去),
∴这条直线的函数表达式为y= $\frac{\sqrt{5}-1}{2}x$.
∵这些矩形右上角的顶点A、B、C…与原点O在同一直线上,
∴可设这条直线的函数表达式为y=kx(k>0),设OD=a,AD=b,则DF=BG=a+b,OG=2a+b,
∴A(a,b),B(2a+b,a+b).将点A、B的坐标代入y=kx(k≠0),得$\begin{cases}b=ak①,\\a+b=k(2a+b)②,\end{cases}$把①代入②,得a+ak=k(2a+ak),化简,得k²+k-1=0,解得k= $\frac{\sqrt{5}-1}{2}$或k= $\frac{-\sqrt{5}-1}{2}$(舍去),
∴这条直线的函数表达式为y= $\frac{\sqrt{5}-1}{2}x$.
19. (8分)解方程:
(1)$100(x-1)^{2}= 121$;
(2)$x^{2}+3x+2= 0$;
(3)$3x(x-1)= 2x-2$;
(4)$(2x+1)^{2}= (x-1)^{2}$.
(1)$100(x-1)^{2}= 121$;
(2)$x^{2}+3x+2= 0$;
(3)$3x(x-1)= 2x-2$;
(4)$(2x+1)^{2}= (x-1)^{2}$.
答案:
(1)100(x-1)²=121,
∴(x-1)²=1.21,
∴x-1=±1.1,
∴x₁=-0.1,x₂=2.1.
(2)x²+3x+2=0,
∴(x+1)(x+2)=0,
∴x+1=0或x+2=0,
∴x₁=-1,x₂=-2.
(3)3x(x-1)=2x-2,
∴3x(x-1)=2(x-1),3x(x-1)-2(x-1)=0,(x-1)(3x-2)=0,
∴x-1=0或3x-2=0,
∴x₁=1,x₂= $\frac{2}{3}$.
(4)(2x+1)²=(x-1)²,
∴2x+1=±(x-1),
∴2x+1=x-1或2x+1=-(x-1),
∴x₁=-2,x₂=0.
(1)100(x-1)²=121,
∴(x-1)²=1.21,
∴x-1=±1.1,
∴x₁=-0.1,x₂=2.1.
(2)x²+3x+2=0,
∴(x+1)(x+2)=0,
∴x+1=0或x+2=0,
∴x₁=-1,x₂=-2.
(3)3x(x-1)=2x-2,
∴3x(x-1)=2(x-1),3x(x-1)-2(x-1)=0,(x-1)(3x-2)=0,
∴x-1=0或3x-2=0,
∴x₁=1,x₂= $\frac{2}{3}$.
(4)(2x+1)²=(x-1)²,
∴2x+1=±(x-1),
∴2x+1=x-1或2x+1=-(x-1),
∴x₁=-2,x₂=0.
查看更多完整答案,请扫码查看


