《2025年课时训练九年级数学上册苏科版江苏人民出版社》

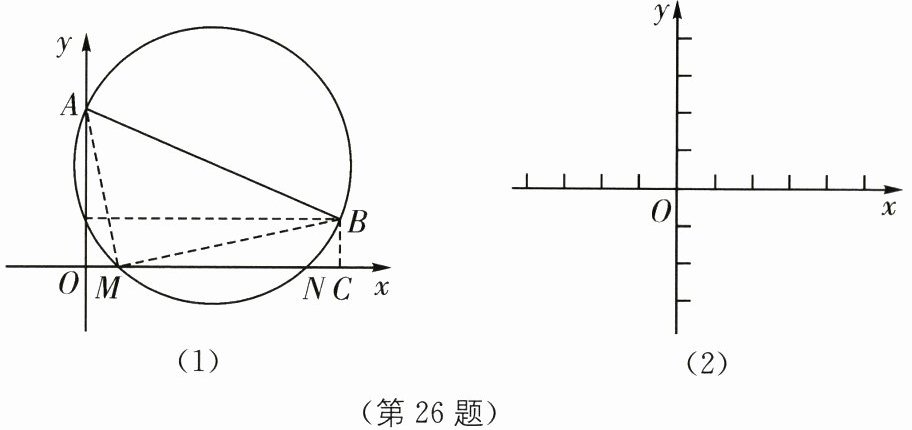
26. (12分)中考新考法解题方法型阅读理解题[新知]19世纪英国著名文学家和历史学家卡莱尔给出了一元二次方程$x^{2}+bx+c= 0$的几何解法:如图(1),在平面直角坐标系中,已知点$A(0,1)$、$B(-b,c)$,以AB为直径作$\odot P$.若$\odot P$交x轴于点$M(m,0)$、$N(n,0)$,则m、n为方程$x^{2}+bx+c= 0$的两个实数根.
[探究](1)由勾股定理,得$AM^{2}= 1^{2}+m^{2},BM^{2}= c^{2}+(-b-m)^{2},AB^{2}= (1-c)^{2}+b^{2}$. 在$Rt△ABM$中,$AM^{2}+BM^{2}= AB^{2}$,所以$1^{2}+m^{2}+c^{2}+(-b-m)^{2}= (1-c)^{2}+b^{2}$. 化简,得$m^{2}+bm+c= 0$. 同理可得____. 所以m、n为方程$x^{2}+bx+c= 0$的两个实数根.
[运用](2)在图(2)中的x轴上画出以方程$x^{2}-3x-2= 0$的两根为横坐标的点M、N.
(3)已知点$A(0,1)$、$B(6,9)$,以AB为直径作$\odot C$. 判断$\odot C$与x轴的位置关系,并说明理由.
[拓展](4)在平面直角坐标系中,已知两点$A(0,a)$、$B(-b,c)$,若以AB为直径的圆与x轴有两个交点M、N,则以点M、N的横坐标为根的一元二次方程是____.

答案：
(1)n²+bn+c=0　[解析]AN²=1²+n²,BN²=c²+(−b−n)²,AB²=(1−c)²+b².在Rt△ABN中,AN²+BN²=AB²,
∴1²+n²+c²+(−b−n)²=(1−c)²+b².化简,得n²+bn+c=0.
(2)先在坐标系内找到A(0,1)、B(3,−2),连接AB,分别以A、B为圆心,以大于$\frac{1}{2}$AB的长为半径画弧,连接两弧的交点与AB交于点P,以点P为圆心,以PA的长为半径画圆，圆与x轴的交点即为点M、N.如图所示:
(3)⊙C与x轴相切.理由如下:由题意,得x²−6x+9=0.
∵Δ=b²−4ac=(−6)²−4×1×9=0,
∴方程x²−6x+9=0有两个相等的实数根,
∴⊙C与x轴只有一个交点,即⊙C与x轴相切.
(4)x²+bx+ac=0　[解析]由勾股定理,得AM²=a²+m²,BM²=(−b−m)²+c²,AB²=(a−c)²+b².在Rt△ABM中,AM²+BM²=AB²,
∴a²+m²+(−b−m)²+c²=(a−c)²+b²,化简,得m²+bm+ac=0.同理可得n²+bn+ac=0,
∴以点M、N的横坐标为根的一元二次方程是x²+bx+ac=0.