《2025年课时训练九年级数学上册苏科版江苏人民出版社》

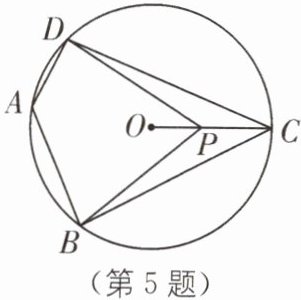
5. 中考新考法 满足条件的结论开放 如图,四边形ABCD内接于$\odot O,∠DAB= 130^{\circ }$,连接OC,点P是半径OC上任意一点,连接DP、BP,则$∠BPD$的度数可能为____°(写出一个即可).

答案： 80（答案不唯一，满足 50°≤∠BPD≤100°即可）

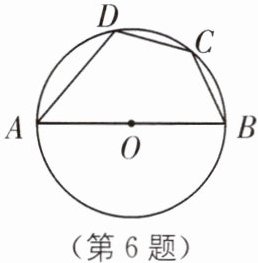
6. 如图,四边形ABCD内接于$\odot O$,AB为直径,$\overset{\frown }{BC}= \overset{\frown }{CD}$.若$∠A= 50^{\circ }$,求$∠B$的度数.

答案： 连接 AC．
∵$\widehat{BC} = \widehat{CD}$，∠BAD = 50°，
∴∠BAC = ∠DAC = $\frac{1}{2}$∠BAD = $\frac{1}{2}$×50° = 25°．
∵AB 为直径，
∴∠ACB = 90°．
∴∠B = 90° - ∠BAC = 90° - 25° = 65°．

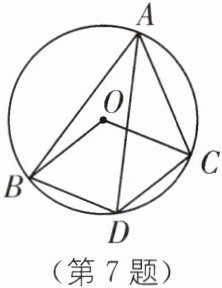
7. 提分优练 如图,四边形ABDC内接于$\odot O,∠BAC= 60^{\circ }$,AD平分$∠BAC交\odot O$于点D,连接OB、OC、BD、CD.
(1)求证:四边形OBDC是菱形;
(2)若$∠ABO= 15^{\circ }$,求$∠ADC$的度数.

答案：
(1)连接 OD．
∵∠BAC = 60°，
∴∠BOC = 120°．
∵AD 平分∠BAC 交⊙O 于点 D，
∴∠BAD = ∠CAD，
∴$\widehat{BD} = \widehat{DC}$．
∴∠BOD = ∠COD = 60°．
∵OB = OD = OC，
∴△BOD 和△COD 都是等边三角形．
∴OB = BD = DC = OC，
∴四边形 OBDC 是菱形．
(2)连接 OA．
∵AO = OB，
∴∠ABO = ∠OAB = 15°．
∴∠AOB = 150°．
∴∠ADB = $\frac{1}{2}$∠AOB = 75°．
∵A、B、D、C 四点共圆，
∴∠BAC + ∠BDC = 180°，
∴∠BDC = 120°，
∴∠ADC = ∠BDC - ∠ADB = 45°．

1. 直线与圆的三种位置关系:①相交:直线与圆有____个公共点时,叫做直线与圆____;②相切:直线与圆有____公共点时,叫做直线与圆相切,这条直线叫做圆的____,唯一的公共点叫做切点;③相离:直线与圆____公共点时,叫做直线与圆相离.

答案： 两　相交　唯一　切线　没有

2. 直线与圆的三种位置关系下圆心到直线的距离与圆的半径的数量关系:设$\odot O的半径为r$,圆心$O到直线l的距离为d$,则:直线$l与\odot O相交\Leftrightarrow d$____$r$;直线$l与\odot O相切\Leftrightarrow d$____$r$;直线$l与\odot O相离\Leftrightarrow d$____$r$.

答案： ＜ = ＞

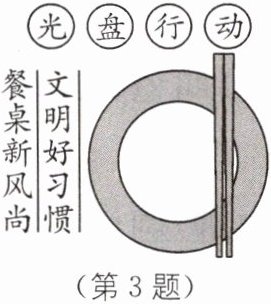
3. 新情境 数学与生活融合 如图是“光盘行动”的宣传海报,图中餐盘与筷子可看成直线和圆的位置关系是( ).

A.相切
B.相交
C.相离
D.平行

答案： B

4. 在$\triangle ABC$中,$CA= CB$,点$O为AB$的中点.以点$C$为圆心、$CO长为半径作\odot C$,则$\odot C与AB$的位置关系是( ).

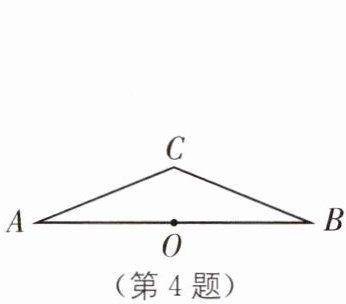
A.相交
B.相切
C.相离
D.不确定

答案： B