6. (2025·宿迁泗阳期中)在Rt△ABC中,∠C= 90°,AC= 6,BC= 8,则这个三角形的外接圆的直径是______。
答案:
10
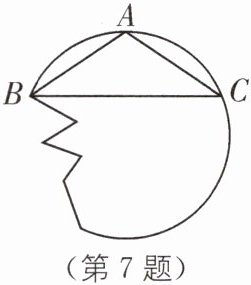
7. 提分优练 中考新考法 无刻度直尺作图 如图,要把破残的圆片复制完整,已知弧上的三点A、B、C。
(1)用尺规作图法,找出弧BC所在圆的圆心O(保留作图痕迹,不写作法);
(2)设△ABC是等腰三角形,底边BC= 24cm,腰AB= 13cm,求圆片的半径R。
(1)用尺规作图法,找出弧BC所在圆的圆心O(保留作图痕迹,不写作法);
(2)设△ABC是等腰三角形,底边BC= 24cm,腰AB= 13cm,求圆片的半径R。

答案:
(1)如图,分别作 AB、AC 的垂直平分线,设交点为 O,则点 O 即为所求圆的圆心.
(2)如图,连接 AO 交 BC 于 E,连接 OB.
∵AB=AC,
∴AE⊥BC,BE=$\frac{1}{2}$BC=12 cm.
在 Rt△ABE 中,AE=$\sqrt{AB^{2}-BE^{2}}$=$\sqrt{13^{2}-12^{2}}$=5(cm).
设⊙O 的半径为 R cm,在 Rt△BEO 中,OB²=BE²+OE²,即 R²=12²+(R - 5)²,
解得 R=$\frac{169}{10}$,
∴所求圆片的半径为$\frac{169}{10}$cm.
(1)如图,分别作 AB、AC 的垂直平分线,设交点为 O,则点 O 即为所求圆的圆心.
(2)如图,连接 AO 交 BC 于 E,连接 OB.
∵AB=AC,
∴AE⊥BC,BE=$\frac{1}{2}$BC=12 cm.
在 Rt△ABE 中,AE=$\sqrt{AB^{2}-BE^{2}}$=$\sqrt{13^{2}-12^{2}}$=5(cm).
设⊙O 的半径为 R cm,在 Rt△BEO 中,OB²=BE²+OE²,即 R²=12²+(R - 5)²,
解得 R=$\frac{169}{10}$,
∴所求圆片的半径为$\frac{169}{10}$cm.
1. 圆周角的定义:顶点在____,并且两边____的角叫做圆周角.
答案:
圆上 都和圆相交
2. 圆周角定理:圆周角的度数等于它所对弧上的____度数的一半,同弧或等弧所对的圆周角____.
答案:
圆心角 相等
3. 如图,点A、B、C在$\odot O$上,$∠ACB= 54^{\circ }$,则$∠ABO$的度数是( ).

A.$54^{\circ }$
B.$27^{\circ }$
C.$36^{\circ }$
D.$108^{\circ }$

A.$54^{\circ }$
B.$27^{\circ }$
C.$36^{\circ }$
D.$108^{\circ }$
答案:
C
4. 中考新考法 满足条件的结论开放 如图,A、B、C是$\odot O$上的三个点,当BC平分$∠ABO$时,能得出结论____(任写一个即可).


答案:
答案不唯一,如∠ABO=∠AOC,CO//AB等.
5. 新情境 构建模型 如图,将一个量角器与一把无刻度直尺水平摆放,直尺的长边与量角器的外弧分别交于点A、B、C、D,连接AB,则$∠BAD$的度数为____.


答案:
52.5° [解析] 设量角器的圆心是O,连接OD、OB.
∵∠BOD=155°-50°=105°,
∴∠BAD= $\frac{1}{2}$∠BOD=52.5°.
∵∠BOD=155°-50°=105°,
∴∠BAD= $\frac{1}{2}$∠BOD=52.5°.
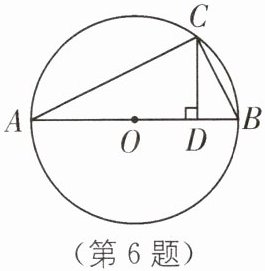
6. 提分优练 (2025·宿迁泗阳期末)如图,AB是$\odot O$的直径,点C在$\odot O$上,且$CD⊥AB$垂足为D.
(1)若$∠A= 30^{\circ }$,则$∠B= $____$^{\circ }$;
(2)若$CD= 4,OD= 3$,求AB的长.
(1)若$∠A= 30^{\circ }$,则$∠B= $____$^{\circ }$;
(2)若$CD= 4,OD= 3$,求AB的长.

答案:
(1)60;
(2)10
(1)60;
(2)10
查看更多完整答案,请扫码查看


